
Concept explainers
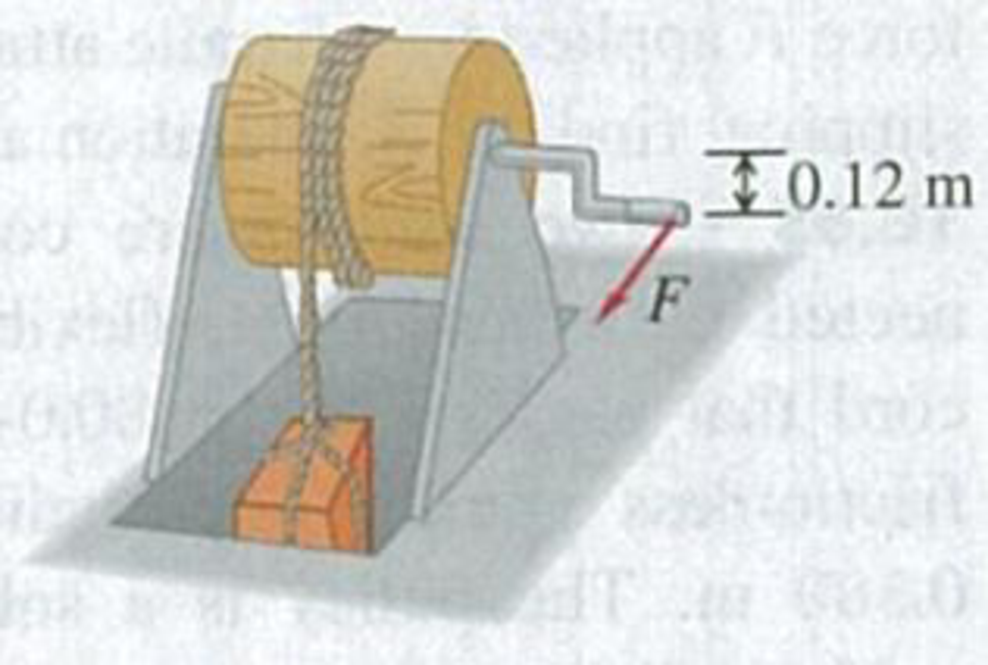
The mechanism shown in Fig. P10.60 is used to raise a crate of supplies from a ship’s hold. The crate has total mass 50 kg. A rope is wrapped around a wooden cylinder that turns on a metal axle. The cylinder has radius 0.25 m and moment of inertia I = 2.9 kg · m2 about the axle. The crate is suspended from the free end of the rope. One end of the axle pivots on frictionless bearings; a crank handle is attached to the other end. When the crank is turned, the end of the handle rotates about the axle in a vertical circle of radius 0.12 m, the cylinder turns, and the crate is raised. What magnitude of the force
Figure P10.60
Want to see the full answer?
Check out a sample textbook solution
Chapter 10 Solutions
University Physics (14th Edition)
Additional Science Textbook Solutions
Physics: Principles with Applications
Physics for Scientists and Engineers with Modern Physics
The Cosmic Perspective Fundamentals (2nd Edition)
Cosmic Perspective Fundamentals
College Physics: A Strategic Approach (3rd Edition)
Lecture- Tutorials for Introductory Astronomy
- Find the net torque on the wheel in Figure P10.23 about the axle through O, taking a = 10.0 cm and b = 25.0 cm. Figure P10.23arrow_forwardA disk with moment of inertia I1 rotates about a frictionless, vertical axle with angular speed i. A second disk, this one having moment of inertia I2 and initially not rotating, drops onto the first disk (Fig. P10.50). Because of friction between the surfaces, the two eventually reach the same angular speed f. (a) Calculate f. (b) Calculate the ratio of the final to the initial rotational energy. Figure P10.50arrow_forwardA student sits on a freely rotating stool holding two dumbbells, each of mass 3.00 kg (Fig. P10.56). When his arms are extended horizontally (Fig. P10.56a), the dumbbells are 1.00 m from the axis of rotation and the student rotates with an angular speed of 0.750 rad/s. The moment of inertia of the student plus stool is 3.00 kg m2 and is assumed to be constant. The student pulls the dumbbells inward horizontally to a position 0.300 m from the rotation axis (Fig. P10.56b). (a) Find the new angular speed of the student. (b) Find the kinetic energy of the rotating system before and after he pulls the dumbbells inward. Figure P10.56arrow_forward
- An electric motor turns a flywheel through a drive belt that joins a pulley on the motor and a pulley that is rigidly attached to the flywheel as shown in Figure P10.37. The flywheel is a solid disk with a mass of 80.0 kg and a radius R = 0.625 m. It turns on a frictionless axle. Its pulley has much smaller mass and a radius of r = 0.230 m. The tension Tu in the upper (taut) segment of the belt is 135 N, and the flywheel has a clockwise angular acceleration of 1.67 rad/s2. Find the tension in the lower (slack) segment of the belt. Figure P10.37arrow_forwardWhy is the following situation impossible? Starting from rest, a disk rotates around a fixed axis through an angle of 50.0 rad in a time interval of 10.0 s. The angular acceleration of the disk is constant during the entire motion, and its final angular speed is 8.00 rad/s.arrow_forwardThe propeller of an aircraft accelerates from rest with an angular acceleration = 4t + 6, where is in rad/s2 and t isin seconds. What is the angle in radians through which thepropeller rotates from t = 1.00 s to t = 6.00 s?arrow_forward
- In testing an automobile tire for proper alignment, a technicianmarks a spot on the tire 0.200 m from the center. He then mountsthe tire in a vertical plane and notes that the radius vector to thespot is at an angle of 35.0 with the horizontal. Starting from rest,the tire is spun rapidly with a constant angular acceleration of 3.00 rad/s2. a. What is the angular speed of the wheel after 4.00 s? b. What is the tangential speed of the spot after 4.00 s? c. What is the magnitude of the total accleration of the spot after 4.00 s?" d. What is the angular position of the spot after 4.00 s?arrow_forwardA disk 8.00 cm in radius rotates at a constant rate of 1200 rev/min about its central axis. Determine (a) its angular speed in radians per second, (b) the tangential speed at a point 3.00 cm from its center, (c) the radial acceleration of a point on the rim, and (d) the total distance a point on the rim moves in 2.00 s.arrow_forwardA war-wolf, or trebuchet, is a device used during the Middle Ages to throw rocks at castles and now sometimes used to fling large vegetables and pianos as a sport. A simple trebuchet is shown in Figure P10.19. Model it as a stiff rod of negligible mass, 3.00 m long, joining particles of mass m1 = 0.120 kg and m2 = 60.0 kg at its ends. It can turn on a frictionless, horizontal axle perpendicular to the rod and 14.0 cm from the large-mass particle. The operator releases the trebuchet from rest in a horizontal orientation. (a) Find the maximum speed that the small-mass object attains. (b) While the small-mass object is gaining speed, does it move with constant acceleration? (c) Does it move with constant tangential acceleration? (d) Does the trebuchet move with constant angular acceleration? (e) Does it have constant momentum? (f) Does the trebuchetEarth system have constant mechanical energy?arrow_forward
- A turntable (disk) of radius r = 26.0 cm and rotational inertia0.400 kg m2 rotates with an angular speed of 3.00 rad/s arounda frictionless, vertical axle. A wad of clay of mass m =0.250 kg drops onto and sticks to the edge of the turntable.What is the new angular speed of the turntable?arrow_forwardA long, uniform rod of length L and mass M is pivoted about a frictionless, horizontal pin through one end. The rod is released from rest in a vertical position as shown in Figure P10.65. At the instant the rod is horizontal, find (a) its angular speed, (b) the magnitude of its angular acceleration, (c) the x and y components of the acceleration of its center of mass, and (d) the components of the reaction force at the pivot. Figure P10.65arrow_forwardA solid sphere of mass m and radius r rolls without slipping along the track shown in Figure P10.83. It starts from rest with the lowest point of the sphere at height h above the bottom of the loop of radius R, much larger than r. (a) What is the minimum value of h (in terms of R) such that the sphere completes the loop? (b) What are the force components on the sphere at the point P if h = 3R? Figure P10.83arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





