Numerical Methods for Engineers
7th Edition
ISBN: 9780073397924
Author: Steven C. Chapra Dr., Raymond P. Canale
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 1, Problem 26P
Beyond fluids, Archimedes' principle has proven useful in geology when applied to solids on the earth's crust. Figure P1.26 depicts one such case where a lighter conical granite mountain “floats on” a denser basalt layer at the earth's surface. Note that the part of the cone below the surface is formally referred to as a frustum. Develop a steady-state force balance for this case in terms of the following parameters: basalt's density
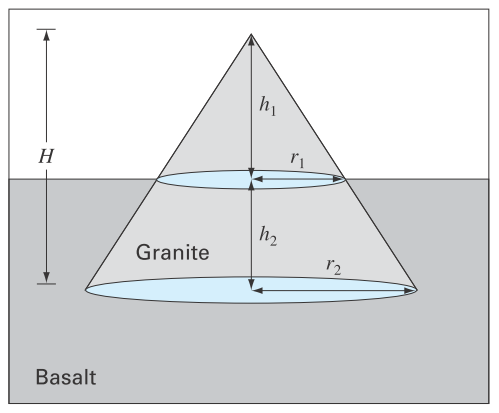
FIGURE P1.26
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Theorem:- if A 2×2 prove i-
At = 2 Re(Q)
where
Q₁
=
(A - I)
21-12
Q2 =
(A-2, 1)
72-71
if 21 = 2
Theorem: show that XCH) = M(E) M" (6) E +
t
Mcfic
S
a
Solution of ODE
-9CA)-
x = ACE) x + g (t) + X (E) - E
5. (a) State the Residue Theorem. Your answer should include all the conditions required
for the theorem to hold.
(4 marks)
(b) Let y be the square contour with vertices at -3, -3i, 3 and 3i, described in the
anti-clockwise direction. Evaluate
に
dz.
You must check all of the conditions of any results that you use.
(5 marks)
(c) Evaluate
L
You must check all of the conditions of any results that you use.
ཙ
x sin(Tx)
x²+2x+5
da.
(11 marks)
Chapter 1 Solutions
Numerical Methods for Engineers
Ch. 1 - Use calculus to solve Eq. (1.9) for the case where...Ch. 1 - 1.2 Repeat Example 1.2. Compute the velocity to ...Ch. 1 - Rather than the linear relationship of Eq. (1.7),...Ch. 1 - For the free-falling parachutist with linear drag,...Ch. 1 - Compute the velocity of a free-falling parachutist...Ch. 1 - 1.6 The following information is available for a...Ch. 1 - The amount of a uniformly distributed radioactive...Ch. 1 - A group of 35 students attend a class in a room...Ch. 1 - A storage tank contains a liquid at depth y, where...Ch. 1 - For the same storage tank described in Prob. 1.9,...
Ch. 1 - 1.11 Apply the conservation of volume (see Prob....Ch. 1 - In our example of the free-falling parachutist,...Ch. 1 - 1.13 Suppose that a spherical droplet of liquid...Ch. 1 - Newtons law of cooling says that the temperature...Ch. 1 - As depicted in Fig. P1.15, an RLC circuit consists...Ch. 1 - 1.16 Cancer cells grow exponentially with a...Ch. 1 - 1.17 A fluid is pumped into the network shown in...Ch. 1 - The velocity is equal to the rate of change of...Ch. 1 - You are working as a crime-scene investigator and...Ch. 1 - 1.21 As noted in Prob. 1.3, drag is more...Ch. 1 - 1.22 As depicted in Fig. P1.22, a spherical...Ch. 1 - As described in Prob. 1.22, in addition to the...Ch. 1 - As depicted in Fig. P1.24, the downward deflection...Ch. 1 - 1.25 Use Archimedes’ principle to develop a...Ch. 1 - Beyond fluids, Archimedes principle has proven...
Additional Math Textbook Solutions
Find more solutions based on key concepts
(a) Make a stem-and-leaf plot for these 24 observations on the number of customers who used a down-town CitiBan...
APPLIED STAT.IN BUS.+ECONOMICS
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
Find all solutions of each equation in the interval .
Precalculus: A Unit Circle Approach (3rd Edition)
First Derivative Test a. Locale the critical points of f. b. Use the First Derivative Test to locale the local ...
Calculus: Early Transcendentals (2nd Edition)
In Exercises 5-36, express all probabilities as fractions.
23. Combination Lock The typical combination lock us...
Elementary Statistics
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- 3. (a) Lety: [a, b] C be a contour. Let L(y) denote the length of y. Give a formula for L(y). (1 mark) (b) Let UCC be open. Let f: U→C be continuous. Let y: [a,b] → U be a contour. Suppose there exists a finite real number M such that |f(z)| < M for all z in the image of y. Prove that < ||, f(z)dz| ≤ ML(y). (3 marks) (c) State and prove Liouville's theorem. You may use Cauchy's integral formula without proof. (d) Let R0. Let w € C. Let (10 marks) U = { z Є C : | z − w| < R} . Let f UC be a holomorphic function such that 0 < |ƒ(w)| < |f(z)| for all z Є U. Show, using the local maximum modulus principle, that f is constant. (6 marks)arrow_forward3. (a) Let A be an algebra. Define the notion of an A-module M. When is a module M a simple module? (b) State and prove Schur's Lemma for simple modules. (c) Let AM(K) and M = K" the natural A-module. (i) Show that M is a simple K-module. (ii) Prove that if ƒ € Endд(M) then ƒ can be written as f(m) = am, where a is a matrix in the centre of M, (K). [Recall that the centre, Z(M,(K)) == {a Mn(K) | ab M,,(K)}.] = ba for all bЄ (iii) Explain briefly why this means End₁(M) K, assuming that Z(M,,(K))~ K as K-algebras. Is this consistent with Schur's lemma?arrow_forward(a) State, without proof, Cauchy's theorem, Cauchy's integral formula and Cauchy's integral formula for derivatives. Your answer should include all the conditions required for the results to hold. (8 marks) (b) Let U{z EC: |z| -1}. Let 12 be the triangular contour with vertices at 0, 2-2 and 2+2i, parametrized in the anticlockwise direction. Calculate dz. You must check the conditions of any results you use. (d) Let U C. Calculate Liz-1ym dz, (z - 1) 10 (5 marks) where 2 is the same as the previous part. You must check the conditions of any results you use. (4 marks)arrow_forward
- (a) Suppose a function f: C→C has an isolated singularity at wЄ C. State what it means for this singularity to be a pole of order k. (2 marks) (b) Let f have a pole of order k at wЄ C. Prove that the residue of f at w is given by 1 res (f, w): = Z dk (k-1)! >wdzk−1 lim - [(z — w)* f(z)] . (5 marks) (c) Using the previous part, find the singularity of the function 9(z) = COS(πZ) e² (z - 1)²' classify it and calculate its residue. (5 marks) (d) Let g(x)=sin(211). Find the residue of g at z = 1. (3 marks) (e) Classify the singularity of cot(z) h(z) = Z at the origin. (5 marks)arrow_forward1. Let z = x+iy with x, y Є R. Let f(z) = u(x, y) + iv(x, y) where u(x, y), v(x, y): R² → R. (a) Suppose that f is complex differentiable. State the Cauchy-Riemann equations satisfied by the functions u(x, y) and v(x,y). (b) State what it means for the function (2 mark) u(x, y): R² → R to be a harmonic function. (3 marks) (c) Show that the function u(x, y) = 3x²y - y³ +2 is harmonic. (d) Find a harmonic conjugate of u(x, y). (6 marks) (9 marks)arrow_forwardLet A be a vector space with basis 1, a, b. Which (if any) of the following rules turn A into an algebra? (You may assume that 1 is a unit.) (i) a² = a, b² = ab = ba = 0. (ii) a²=b, b² = ab = ba = 0. (iii) a²=b, b² = b, ab = ba = 0.arrow_forward
- No chatgpt pls will upvotearrow_forward= 1. Show (a) Let G = Z/nZ be a cyclic group, so G = {1, 9, 92,...,g" } with g": that the group algebra KG has a presentation KG = K(X)/(X” — 1). (b) Let A = K[X] be the algebra of polynomials in X. Let V be the A-module with vector space K2 and where the action of X is given by the matrix Compute End(V) in the cases (i) x = p, (ii) xμl. (67) · (c) If M and N are submodules of a module L, prove that there is an isomorphism M/MON (M+N)/N. (The Second Isomorphism Theorem for modules.) You may assume that MON is a submodule of M, M + N is a submodule of L and the First Isomorphism Theorem for modules.arrow_forward(a) Define the notion of an ideal I in an algebra A. Define the product on the quotient algebra A/I, and show that it is well-defined. (b) If I is an ideal in A and S is a subalgebra of A, show that S + I is a subalgebra of A and that SnI is an ideal in S. (c) Let A be the subset of M3 (K) given by matrices of the form a b 0 a 0 00 d Show that A is a subalgebra of M3(K). Ꮖ Compute the ideal I of A generated by the element and show that A/I K as algebras, where 0 1 0 x = 0 0 0 001arrow_forward
- (a) Let HI be the algebra of quaternions. Write out the multiplication table for 1, i, j, k. Define the notion of a pure quaternion, and the absolute value of a quaternion. Show that if p is a pure quaternion, then p² = -|p|². (b) Define the notion of an (associative) algebra. (c) Let A be a vector space with basis 1, a, b. Which (if any) of the following rules turn A into an algebra? (You may assume that 1 is a unit.) (i) a² = a, b²=ab = ba 0. (ii) a² (iii) a² = b, b² = abba = 0. = b, b² = b, ab = ba = 0. (d) Let u1, 2 and 3 be in the Temperley-Lieb algebra TL4(8). ገ 12 13 Compute (u3+ Augu2)² where A EK and hence find a non-zero x € TL4 (8) such that ² = 0.arrow_forwardQ1: Solve the system x + x = t², x(0) = (9)arrow_forwardBetween the function 3 (4)=x-x-1 Solve inside the interval [1,2]. then find the approximate Solution the root within using the bisection of the error = 10² method.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Trigonometry - Harmonic Motion - Equation Setup; Author: David Hays;https://www.youtube.com/watch?v=BPrZnn3DJ6Q;License: Standard YouTube License, CC-BY
Simple Harmonic Motion - An introduction : ExamSolutions Maths Revision; Author: ExamSolutions;https://www.youtube.com/watch?v=tH2vldyP5OE;License: Standard YouTube License, CC-BY