Elements Of Electromagnetics
7th Edition
ISBN: 9780190698614
Author: Sadiku, Matthew N. O.
Publisher: Oxford University Press
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Question
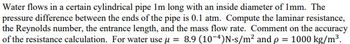
Transcribed Image Text:**Educational Content: Understanding Laminar Flow in Cylindrical Pipes**
In this example, we explore the flow of water through a cylindrical pipe to better understand key concepts in fluid dynamics such as laminar resistance, the Reynolds number, entrance length, and mass flow rate.
**Problem Statement:**
Water flows through a cylindrical pipe that is 1 meter long with an inside diameter of 1 millimeter. The pressure difference between the ends of the pipe is 0.1 atm. We are tasked with computing the following:
- Laminar resistance
- Reynolds number
- Entrance length
- Mass flow rate
Finally, we need to comment on the accuracy of the resistance calculation.
**Given Data:**
- Viscosity of water, \( \mu = 8.9 \times 10^{-4} \, \text{N}\cdot\text{s/m}^2 \)
- Density of water, \( \rho = 1000 \, \text{kg/m}^3 \)
**Calculation Steps:**
1. **Laminar Resistance:**
- The laminar flow resistance can be calculated using fluid dynamics equations specific to cylindrical pipes.
2. **Reynolds Number:**
- This dimensionless number is calculated to determine the flow regime (laminar or turbulent) and is given by \( \text{Re} = \frac{\rho v D}{\mu} \), where \( v \) is the flow velocity and \( D \) is the diameter.
3. **Entrance Length:**
- The entrance length, a measure of how long it takes for the fluid flow to develop fully, can be computed utilizing relationships involving the Reynolds number.
4. **Mass Flow Rate:**
- Using the continuity equation and given properties, the mass flow rate is determined by \( \dot{m} = \rho A v \), where \( A \) is the cross-sectional area.
**Comment on Accuracy:**
- The accuracy of the resistance and other calculated parameters can be evaluated by comparing with empirical data or using validation techniques. It's crucial to consider assumptions made, such as perfectly smooth pipe walls and constant properties.
**Conclusion:**
This example illustrates fundamental principles for analyzing fluid motion in pipes, emphasizing precise computations and practical considerations essential in engineering and physics applications.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Question 3 Water (p = 1000 kg/m³, μ = 1.12 x 10-3 Ns/ m²) flows through a 0.01-m-diameter pipe at a velocity of 2 m/s. The length of the pipe is 40 m. A pump is used to maintain the flow from one reservoir to another reservoir as shown. The following data are available: KL elbow = 1.5, Kentrance = 0.5, Kexit = 1.0. Elbow Pump Elbow Figure Q1 Note that the entrance and exit are at the same elevation. The free surfaces of the reservoirs are also at the same elevation. (a) Calculate the total head losses in the pipe.arrow_forwardanswer first item onlyarrow_forwardWorking for an engineering consultancy firm, your knowledge of fluid dynamics is required to design a new safety feature for a high-pressure air line in a factory. The air line takes the form of a cylindrical pipe of diameter 150 mm, which is designed to operate between 0.45 MPa and 0.76 MPa. At the end of the pipe a burs9ng disk is placed so that, if the pressure exceeds the maximum opera9ng pressure, the air is vented to atmosphere rather than over-pressuring the chemical reac9on vessel (Figures 4a and 4b). In this ques9on, you should treat the flow as quasione-dimensional and inviscid. The air in the surrounding atmosphere is at 101 kPa and 298 K. a) You have a choice of five disks which can withstand the following forces across them before burs9ng: 10.5 kN, 11.0 kN, 11.5 kN, 12.0 kN, 12.5 kN. Which of these burs9ng disks would you recommend, and why? b) Due to an over-pressurisa9on of the air line, the disk bursts at 9me t = 0. At what pressure in the air line will this occur? c)…arrow_forward
- 200 pm 0.12 cm Fluid Stationary cylinder 4 In regions far from the entrance, fluid flow through a circular pipe is one-dimensional, and the velocity profile for laminar flow is given by u(r) = Umax(1 - r/R9), where R is radius of the pipe, r is the radial distance from the center of the pipe, and Umax is the maximum flow velocity, which occurs at the center. Obtain (a) a relation for the drag force applied by the fluid on a section of the pipe length L and (b) the value of the drag force for water flow at 20°C with R = 0.08 m, L = 15 m, Umax = 3 m/s, and u = 0.0010 kg/m.s. %3Darrow_forwardLiquid flows at a rate of 1.5 L/min in a circular tube with a diameter of 5 mm. inside a circular tubeThe vascular endothelial cells are attached. One cell has a surface area of 500 μm2. To be attached to the inner wall of the tube. What force does one cell have to withstand? The viscosity of the liquid is 1.2 cP = 0.0012 Pass.arrow_forwardQuestion 5 Water exits from a large vessel through a smooth pipe, with a length L = 7 m and an internal diameter D = 5 cm, as shown in Figure Q5. The loss coefficient at the pipe inlet is KL,1 = 0.8 and at the outlet is KL,2 = 1. The flowrate out of the pipe is 10 L/s. The density and viscosity of water are p = 1000kg/m³ and μ = 1 mPa.s. a) Find the Reynolds number in the pipe b) Find the friction factor in the pipe, fp. If you use the Moody diagram, include this in your answer clearly showing how you calculated fp. (A Moody diagram is available at the end of this exam paper.) c) What is pressure at the pipe inlet, p₁? (Note: the pressure difference between p2 and p₁ is equal to the total pressure drop along the pipe, including minor and major losses.) P1 L • P₂ Figure Q5: A straight pipe allows water to exit from a pipe to the atmosphere.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education 
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY