
Computer Networking: A Top-Down Approach (7th Edition)
7th Edition
ISBN: 9780133594140
Author: James Kurose, Keith Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
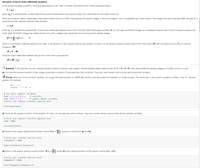
Transcribed Image Text:Derivation of the Dc motor differential equations
Under typical operating conditions, the torque generated by a DC motor is directly proportional to the cumrent passing through it
T-kai
where kis a proportionality constant determined by the characteristics of the specific motor. This relationship fails for large values of i.
When the armature ratates, z generates a back electromotive force (back EMF) that opposes the applied valtage. In the circuit diagram, this is represented by a mator symbol. The voltage drop dua to the back EMF, denoted e, is
proportional to the rotational velocity af the armature
e-kp
where k, is a constant of proportionality. Ta derive the relationship between the current i and the motor shaftt angular position 0. yau can apply KirchhofT's voltage law and Nowton's second law in terms of torques acting on the
motor shaft. Kirchhoff's voltage law implies that the sum at the vatage drops across the circuit must equal tha applied voltage:
iR +
(1)
where v is the electric potential applied to the motor. In the absence af other applied torques, the equation aft motion can be derived by balancing the inertia of the motor shaft (Jõ) with the applied torque (7) and mictional
resistance (k
Jõ-T-R
Using the linear relationship batwoen torque and curent, this is equivalent to:
Jõ + Bồ -i
(2)
Exerolce. In this axercise, you will compute transfer functions of the DC motor system. Assume that the system starts at rest (i-i-0-0-0). Also, assume that the applied voltage is a function of time v-ve).
(a) Compute the Laplace transform af the voltage conservation equation (1) and apply the initial condiions Type your result below in terms af the defined symbolic variables.
Pro-tip: When you write a symbolic equatian, you assign the whole aquation to a MATLAB variable using the assignment aperator"-" (singie equals). The equals sign in the symbolic equation is written using "--" (double
equals). For exampie:
syms y b
lineartay
* use these sysbolic variables
syns LRke Bkn
syms Theta ISV
* write your laplace transform equation here
* Constants
* Laplace donaln varlables
%checkEgn1(egn1)
(b) Compute the Laplace transform of the equation of motion (2) and apply the initial condions. Type your answer below in tems of the defined symbolic variables.
* write your laplace transform equation here
egn2 - NaN,
IcheckEgn2(egn2)
(0) Salve for the angular displacement transfer funcion Gs)
es
using your results from (a) and (D).
* write your transfer function here
Thetaoverv - Na,
XcheckThetaoverv( Thetadverv)
(d) Solve for tha angular velocity transter function lis
where 2 is the Laplace transform of the angular velocity a) -).
* write your transfer function here
Onegaoverv - NaN;
Xcheckonegaoverv(Onegaoverv)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- Determine the transfer function, of the rotational mechanical system shown in T(s) Figure Q2. The variables 6,(t) and 02(t) refer to angular displacement of motion, while T(t) is a torque applied to the system. Given the value of spring, damping coefficient and inertia as; J: 5 kg-m? Di: 5 N-m-s/rad J2: 10 kg-m? K : 6 N-m/rad K2 : 5 N-m/rad D::4 N-m-s/rad D3:2 N-m-s/rad T(t) e,(1) D2 K2 0000 D1 D3 Figure Q2arrow_forwardProblem (1) For the circuit shown in fig. find the current supplied by the battery by using delta/star transformation 400 www 2002 500 30 V 2002 www 30Ω www 5Ω wwarrow_forward19arrow_forward
- Using the matlab computer software, write the code to plot the graph y = e" R3 as a surface on You can use a set of values between -5 to 5 for your operationsarrow_forward3. Apply Thèvenin's theorem to find Vo in the circuit of Fig. 42 1Ω ww 5Ω 3 A 16 2 10 Ω 12 Varrow_forwardA uniform Simply-supported beam is found to vibrate in its first mode with the amplitude of 12 mm at its center. Assume E=200 GPa, I = 1000 mm“ , p=7500 kg/m², A=50mm² and L=2 m. Determine the maximum bending moment in the beam. Also find the first three natural frequencies.arrow_forward
- The em.f. of a primary cell is x V, when it is shorted then it gives a current of y A. Calculate internal resistance! of primary cell. Take the x and y from user in java programming languagearrow_forwardwhere is it demonstrated that the Hamiltonian circuit's tour length is, at most, 4/3 times that of the ideal TSP trip.arrow_forward19. For the network of Fig. 6.82 D, find: a. The voltage V. b. The current /2. c. The current I,. d. The power to the 12 kQ resistor. 12 kΩ 18 kN 48 V Is + v - 3 kN 12arrow_forward
- 2. calculates the trajectory r(t) and stores the coordinates for time steps At as a nested list trajectory that contains [[xe, ye, ze], [x1, y1, z1], [x2, y2, z2], ...]. Start from time t = 0 and use a time step At = 0.01; the last data point in the trajectory should be the time when the oscillator "hits the ground", i.e., when z(t) ≤ 0; 3. stores the time for hitting the ground (i.e., the first time t when z(t) ≤ 0) in the variable t_contact and the corresponding positions in the variables x_contact, y_contact, and z_contact. Print t_contact = 1.430 X_contact = 0.755 y contact = -0.380 z_contact = (Output floating point numbers with 3 decimals using format (), e.g., "t_contact = {:.3f}" .format(t_contact).) The partial example output above is for ze = 10. 4. calculates the average x- and y-coordinates 1 y = Yi N where the x, y, are the x(t), y(t) in the trajectory and N is the number of data points that you calculated. Store the result as a list in the variable center = [x_avg, y_avg]…arrow_forwardHi! Please can I have the solution for this questionarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON
Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science
Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning
Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning
Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education
Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY
Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY

Computer Networking: A Top-Down Approach (7th Edi...
Computer Engineering
ISBN:9780133594140
Author:James Kurose, Keith Ross
Publisher:PEARSON

Computer Organization and Design MIPS Edition, Fi...
Computer Engineering
ISBN:9780124077263
Author:David A. Patterson, John L. Hennessy
Publisher:Elsevier Science

Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:9781337569330
Author:Jill West, Tamara Dean, Jean Andrews
Publisher:Cengage Learning

Concepts of Database Management
Computer Engineering
ISBN:9781337093422
Author:Joy L. Starks, Philip J. Pratt, Mary Z. Last
Publisher:Cengage Learning

Prelude to Programming
Computer Engineering
ISBN:9780133750423
Author:VENIT, Stewart
Publisher:Pearson Education

Sc Business Data Communications and Networking, T...
Computer Engineering
ISBN:9781119368830
Author:FITZGERALD
Publisher:WILEY