
Concept explainers
The Lo Shu Magic Square is a grid with 3 rows and 3 columns shown below.
The Lo Shu Magic Square has the following properties:
- The grid contains the numbers 1 – 9 exactly
- The sum of each row, each column and each diagonal all add up to the same number.
This is shown below:
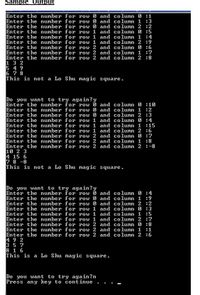
Write a program that simulates a magic square using 3 one dimensional parallel arrays of integer type. Do not use two-dimensional array.
Each one the arrays corresponds to a row of the magic square.
The program asks the user to enter the values of the magic square row by row and informs the user if the grid is a magic square or not.
Processing Requirements - c++
Use the following template to start your project:
#include<iostream>
using namespace std;
// Global constants
const int ROWS = 3; // The number of rows in the array
const int COLS = 3; // The number of columns in the array
const int MIN = 1; // The value of the smallest number
const int MAX = 9; // The value of the largest number
// Function prototypes
bool isMagicSquare(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size);
bool checkRange(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size, int min, int max);
bool checkUnique(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size);
bool checkRowSum(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size);
bool checkColSum(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size);
bool checkDiagSum(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size);
void fillArray(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size);
void showArray(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size);
int main()
{
/* Define a Lo Shu Magic Square using 3 parallel arrays corresponding to each row of the grid */
int magicArrayRow1[COLS], magicArrayRow2[COLS], magicArrayRow3[COLS];
// Your code goes here
return 0;
}
// Function definitions go here
Create and use following functions:
- void fillArray(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size) - Accepts 3 int arrays and a size as arguments, and fills the arrays out with values entered by the user. First argument corresponds to the first row of the magic square, second argument to the second row and the third argument to the third row of the magic square
- void showArray(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size) - accepts 3 int arrays and a size as arguments and displays their content.
- bool isMagicSquare(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size) - accepts 3 int arrays and a size as arguments and returns true if all the requirements of a magic square are met. Otherwise, it returns false. First argument corresponds to the first row of the magic square, second argument to the second row and the third argument to the third row of the magic square.
- bool checkRange(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size, int min, int max) - accepts 3 int arrays, a size and a min and max value as arguments and returns true if the values in the arrays are within the specified range min and max. Otherwise, it returns false. First argument corresponds to the first row of the magic square, second argument to the second row and the third argument to the third row of the magic square.
- bool checkUnique(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size) - accepts 3 int arrays and a size as arguments, and returns true if the values in the arrays are unique (only one occurrence of numbers between 1-9). Otherwise, it returns false. First argument corresponds to the first row of the magic square, second argument to the second row and the third argument to the third row of the magic square.
- bool checkRowSum(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size) - accepts 3 int arrays and a size as arguments and returns true if the sum of the values in each of the rows are equal. Otherwise, it returns false. First argument corresponds to the first row of the magic square, second argument to the second row and the third argument to the third row of the magic square.
- bool checkColSum(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size) - accepts 3 int arrays and a size as arguments and returns true if the sum of the values in each of the columns are equal. Otherwise, it returns false. First argument corresponds to the first row of the magic square, second argument to the second row and the third argument to the third row of the magic square.
- bool checkDiagSum(int arrayRow1[], int arrayRow2[], int arrayRow3[], int size) - accepts 3 int arrays and a size as arguments and returns true if the sum of the values in each of the array's diagonals are equal. Otherwise, it returns false. First argument corresponds to the first row of the magic square, second argument to the second row and the third argument to the third row of the magic square.
please use the code template supplied and include the function definitions at the bottom. Thank you!
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

- I have an array of the first 50 Fibonacci numbers in the picture. Your program should ask the user for a number between 5 and 21. Using that input as a location in the array, with that location and the next three locations (for example base, base+1, base+2 and base+3) you will multiply the outer values, base and base+3, (the first and last of the four). Do the same for the inner values (base+1 and base+2 multiplied) and then double that value. These two values form the two sides of a right triangle. Now find the hypotenuse. Remember the Pythagorean theorem, which says a2 + b2 = c2. Our two sides are a and b, so we square each of them (remember a * a = a2, so just multiply each value by itself) and add them together. That gives you c2. Now all you need do is take the square root of that sum. Given that the sqrt method normally returns a floating-point value (a double), we must force it to return a long integer for us in this case, so use the following line (with your own…arrow_forwardProblem 1: Complete the sumOfDiagonals method in SumOfDiagonals.java to do the following: The method takes a 2D String array x as a parameter and returns no value. The method should calculate and print the sum of the elements on the major diagonal of the array x. In order to have a major diagonal, the array passed into the method should be a square (n-by-n), if it's not a square your program should handle that situation by throwing an exception. (Do Not worry about ragged arrays) If the array is a square, but there is a non-integer value on the major diagonal, your program should handle that situation by throwing an exception. When handling the exceptions, be as specific as you can be, (i.e. Do Not just use the Exception class to handle all exceptions in one catch block). Make the proper calls to the sumOfDiagonals method from the main method to test your sumOfDiagonals method on all the String arrays provided in the main method.arrow_forwardProblem Description - JAVA PROGRAMMING Use a Two-dimensional (3x3) array to solve the following problem: Write an application that inputs nine numbers, each of which is between 1 and 10, inclusive. Display the array after the user inputs each value. Rotate/flip the array by changing places. Make the rows columns and vice versa. You have to move the elements to their new locations. Remember to validate the input and display an error message if the user inputs invalid data. Documentation and the screenshot(s) of the results. Example: 1 2 3 4 5 6 7 8 9 the result will be : 1 4 7 2 5 8 3 6 9arrow_forward
- Program: Using a multidimensional array, create a triangular-shaped array. You will ask the user how many lines they want to see and then create the array, fill it, and then print it. You will fill the array with one 1 in the first row, two 2’s in the second row, etc. This should work for any integer that the user enters. (Just because I am starting on 1 does not mean row 0 was skipped.) You must: use a loop to create the array shape. You must: use nested for loops to fill the array and to print the values back to the screen. Your program should print as shown below. Example Output: How many lines would you like in your triangle? >>>9 1 2 2 3 3 3 4 4 4 4 5 5 5 5 5 6 6 6 6 6 6 7 7 7 7 7 7 7 8 8 8 8 8 8 8 8 9 9 9 9 9 9 9 9 9 If your code looks like the code below, it is not what I’m asking for. The code below is making a square multidimensional array, not a triangular one. The code below is just leaving certain spots empty so that it looks like a triangle. I will ask you…arrow_forwardIn this project you will generate a poker hand containing five cards randomly selected from a deck of cards. The names of the cards are stored in a text string will be converted into an array. The array will be randomly sorted to "shuffle" the deck. Each time the user clicks a Deal button, the last five cards of the array will be removed, reducing the size of the deck size. When the size of the deck drops to zero, a new randomly sorted deck will be generated. A preview of the completed project with a randomly generated hand is shown in Figure 7-50.arrow_forwardWrite a program that reads student scores into an array, gets the best score, and then assigns grades based on the following scheme: • Grade is A if score is • Grade is B if score is • Grade is C if score is • Grade is D if score is • Grade is F otherwise. best - 10 best - 20; best - 30; best - 40; The program prompts the user to enter the total number of students, then prompts the user to enter all of the scores, and concludes by displaying the gradesarrow_forward
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education





