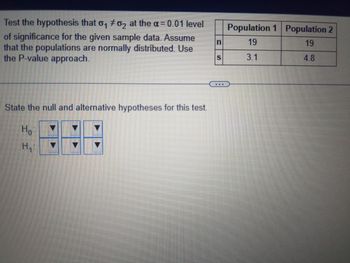
**Hypothesis Testing Using P-Value Approach****Objective:**Test the hypothesis that the population standard deviations \( \sigma_1 \neq \sigma_2 \) at the \( \alpha = 0.01 \) level of significance for the given sample data. Assume that the populations are normally distributed. **Data:**- **Population 1:** - Sample size (\( n \)): 19 - Sample standard deviation (\( s \)): 3.1- **Population 2:** - Sample size (\( n \)): 19 - Sample standard deviation (\( s \)): 4.8**Instructions:**1. **State the Hypotheses:** - **Null Hypothesis (\( H_0 \)):** \( \sigma_1 = \sigma_2 \) - **Alternative Hypothesis (\( H_1 \)):** \( \sigma_1 \neq \sigma_2 \) 2. **Use the P-value Approach:** - Calculate the test statistic. - Determine the p-value. - Compare the p-value to the significance level (\( \alpha = 0.01 \)). - Draw conclusions based on the comparison.**Note:** Ensure data is normally distributed to correctly apply the test.

For testing the difference in standard deviations, hypothesis: H0: σ1= σ2 H1: σ1=! σ2

Answered: Test the hypothesis that 0₁ #02 at the…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Similar questions

Test the claim below about the mean of the differences for a population of paired data at the level of significance a. Assume the samples are random and dependent, and the populations are normally distributed. Claim: Hg = 0; = 0.01. Sample statistics: d = 2.9, sg = 8.03, n = 7 Identify the null and alternative hypotheses. Choose the correct answer below. O A. Ho: Ha s 0 B. Ho: Hd 0 Ha: Hd 20 O D. Ho: Hd #0 C. Ho: Hd = 0 Ha: Hd #0 Ha: Hd = 0 O F. Ho: Hd >0 Ha: Hd s0 E. Ho: Hd 20 Ha: Hd <0
A study was done using a treatment group and a placebo group. The results are shown in the table. Assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. Complete parts (a) and (b) below. Use a 0.10 significance level for both parts. a. Test the claim that the two samples are from populations with the same mean. What are the null and alternative hypotheses? OA. Ho H1 H2 H₁: H1 H2 o C. Ho: H = 2 H₁: H1 H2 OB. Ho: H1 H2 H1 H1 H2 OD. Ho H1 H2 H₁: 12 Treatment Placebo μ H1 H2 n 27 31 X 2.35 2.65 S 0.95 0.55
Test the claim below about the mean of the differences for a population of paired data at the level of significance a. Assume the samples are random and dependent, and the populations are normally distributed. Claim: 0 Ha: Hd s0 O E. Ho: Hd s0 Ha: Ha Ho: Hd 20 Hai Hd 0 The test statistic is t= 1.94 (Round to two decimal places as needed.) The critical value(s) is(are) to %3D (Round to two decimal places as needed. Use a comma to separate answers as needed.)
Question Help Instructor-created question Sham Magnet H1 Researchers conducted a study to determine whether magnets can affect back pain. The results are shown in the table for the treatment (with magnets) group and the sham (or placebo) group. The results are a measure of reduction in back pain. Assume that the two samples H are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. Use a 0.05 significance level to test thế claim that those treated with magnets have a different mean reduction in than those given a sham treatment. P2 10 10 0.54 0.45 5. 0.62 1.49 pain What are the null and alternative hypotheses? O A. Ho: H1 H2 O C. Ho H1 H2 O D. Ho: H1= H2 H1 P1 H2 ents Upper critical value is: (Round to three decimal places as needed.) Lower critical value is: (Round to three decimal places as needed.) cess Library Click to select your answer(s) and then click Check Answer. Clear All Check…
sanjay
I need help on this practice problem
Test the claim below about the mean of the differences for a population of paired data at the level of significance a. Assume the samples are random and dependent, and the populations are normally distributed. Claim: H. 20; a = 0.05. Sample statistics: d= - 2.2, s, = 1.5, n= 14 Identify the null hypothesis by writing its complement. OB. Ho: Ha s0 OA Ho: Ha #0 H: Ha =0 OD. Ho: Ha0 VE. Ho: Ha20 Ha: Hd <0 The test statistic is t= (Round to two decimal places as needed.)
Suppose that you want to perform a hypothesis test based on a simple random paired sample to compare the means of two populations. For each part, decide whether you would use the paired t-test, the pairedWilcoxon signed-rank test, or neither of these tests. Preliminary data analyses of the sample of paired differences suggest that the distribution of the paired-difference variable is a. approximately normal.b. highly skewed; the sample size is 20.c. symmetric bimodal
Find test statistic and P value And state conclusion for the test
Determine P-Value.
Use a y-test to test the claim o 35 H, o35 hir winga H, o>35 Identify the test statistic. 18.652 (Round to three decimal places as needed.) me Identify the critical value(s). nts (Round to three decimal places as needed. Use a comma to separate answers as needed.) t: C k Contents edia Library View an example Get more help - Clear all Check answer Help me solve this Plan ior SucceSE 72°F A a a 99+ P Type here to search 10/05/17 Delete PrtSc Insert F12 E11
Thanks

SEE MORE QUESTIONS

Recommended textbooks for you

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

Elementary Statistics: Picturing the World (7th E…

Statistics

ISBN:

9780134683416

Author:

Ron Larson, Betsy Farber

Publisher:

PEARSON

The Basic Practice of Statistics

Statistics

ISBN:

9781319042578

Author:

David S. Moore, William I. Notz, Michael A. Fligner

Publisher:

W. H. Freeman

Introduction to the Practice of Statistics

Statistics

ISBN:

9781319013387

Author:

David S. Moore, George P. McCabe, Bruce A. Craig

Publisher:

W. H. Freeman

SEE MORE TEXTBOOKS

Test the hypothesis that 0₁ #02 at the a= 0.01 level of significance for the given sample data. Assume that the populations are normally distributed. Use the P-value approach. State the null and alternative hypotheses for this test. Ho: H₁: S Population 1 Population 2 19 19 3.1 4.8