
Suppose that there is a firm that produces chairs and the firm receives an order for 80 chairs. The
firm has two resources available to it. The first is a (human) worker, who must be paid $18 for
each hour they spend producing chairs. The second is a robot, that costs $15 of inputs (including
electricity and maintenance) for each hour it works. Chairs produced by either method are
identical and of equivalent quality.
Assume that the use of these two inputs is completely independent. This means that the number
of hours of robot-work does not affect the productivity of the worker, and vice versa.
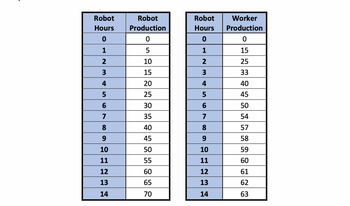
The production of chairs based upon the numbers of hours of each of the inputs used is given
below. For example, 2 hours of robot time will produce 10 chairs. 7 hours of worker time will
produce 54 chairs.
Please use the image provided to answer the following:
1) Do any of the inputs in this example exhibit diminishing returns to scale? If so, which
and how do you know? If not, how do you know?
2) Assume that the sale price of chairs is always sufficiently high that it is profitable to fulfill this
80-chair order. The firm needs to make 80 chairs to fulfill its order. Assume also that the firm is
profit maximizing (& therefore cost minimizing). What combinations of robot and worker hours must they use to minimize costs?(Use the equation that must be true for cost minimization)
3) Now suppose that the local economy increases the minimum wage, and the price of an hour of
a worker’s time increases from $18 to $27. What does the principle of substitution say should happen to the firm’s use of (i) worker hours and (ii) robot hours?
4) Continue to assume that it will be profitable to produce the 80 chairs and that the firm is profit-
maximizing. With this new price for worker hours, what is the new combination of robot and worker
hours that will minimize the cost of producing (at least) 80 chairs? Show your work. (Use
the equation that must be true for cost minimization)
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

- A company produces commercials. A 2-minute commercial, for example, needs exactly 5 minutes of filming and 8 minutes of editing. Let x1 denote the minutes of filming and x2 denote the minutes of editing. a) Write down the production function and state whether it has increasing, constant, or decreasing returns to scale b) Suppose that filming costs $45 per minute and editing costs $10 per minute. To produce a 5-minute commercial, how many minutes of filming and how many minutes of editing is needed to minimize cost? c) Suppose that filming costs w1 per minute and editing costs w2 per minute. Let y denote the length (in minutes) of commericals produced. derive the conditional factor demand functions x1(w1,w2,y) and x2(w1,w2,y) and its cost function c(w1,w2,y)arrow_forwardSuppose the production of Scooby Snacks at x units of labor and y units of capital is given by the Cobb-Douglas production function P(x, y) = kx"y" where m, n, k are known positive constants and m+ n = 1. The company can spend only p dollars for the production of Scooby Snacks. The cost of one unit of labor is b dollars, while the cost of one unit of capital is c dollars. Using Lagrange multipliers, find an expression for x and y where maximum production will occur?arrow_forwardA T-shirt screener can screen t-shirts (q) in two different ways. He can either use a fast screening machine (F) or a slow screening machine (S). Screen use is defined in terms of ”hours” running. His production function is f(F, S) = 10F + 6S. (a) The screener wants to be able to produce 120 shirts. List three feasible and efficient production plans (combinations of inputs) for doing this. (b) Graph the screener’s isoquant curve for q = 120. (c) The hourly cost of using the fast machine is $800 and the hourly cost of the slow machine is $200. What is the cost minimizing (optimal) combination of inputs for producing 120 shirts? (d) Suppose the screener must now produce 400 shirts. What is the cost minimizing combination of inputs?arrow_forward
- Suppose a firm uses a single input to produce a single output according to a production function f(x) = 10√x where x is the number of units of input. The output initially sells for £120 per unit. The input costs £20 per unit. A change in the market causes the product price to increase from £120 per unit to £200 per unit, all else equal. How does this change in product price affect the firm's profit maximizing level of profits? a. Profits increase by £16,000 Ob. Profits do not change Profits increase by £8,000 d. None of the other answers is correct Profits increase by £9,000 f. Profits increase by £18,000 g. Profits increase by £50,000 h. Profits increase by £32,000 C. e.arrow_forwardCAN YOU ANSWER QUESTIONS 1 & 2 FOR ME? Suppose that you are the manager of a company that vaccinates human beings for biological diseases. Your company uses two inputs to produce vaccinations: physicians and laboratories. However, this is a short-run analysis where physicians are variable but laboratories are fixed. Suppose that each physician costs $500 per day (for an annual salary of about $175,000) and the daily cost for the laboratory is $1,500 (for rental cost of about $547,500 per year). In the short run, your company has 1 laboratory. The following table presents potential daily production levels with requisite input combinations. Physicians Laboratories Vaccinations (Q) TC TFC TVC MC ATC AFC AVC 0 1 0 1500 1500 0 - - - - 3 1 1 3000 1500 1500 1500 3000 1500 1500 5 1 2 4000 1500 2500 1000 2000 750 1250 6 1 3 4500 1500 3000 500 1500 500 1000…arrow_forwardA software firm has only two inputs to production: domestic programmers based in the firm's U.K. office and international programmers working from home in low-cost countries. The two types of programmers are perfect substitutes but domestic programmers are more productive due to better communication in the office. The production function is: S=2D + I Where S is the amount of software written, D is the number of domestic programmers and I is the number of international programmers. Programmers can work part-time, so hiring 0.3 of a programmer would be possible. (a) The firm must produce 10 pieces of software this year. Show the firm's isoquant in a suitably labelled graph. Put "domestic programmers" on the vertical axis and "international programmers" on the horizontal axis. Label each axis from 0 to 10. (b) A domestic programmer can be hired for £100,000 per year. An international programmer can be hired for £60,000 per year. On the same graph, show the different combinations of…arrow_forward
- please only solve part d, e, farrow_forwardQuestion 5: Suppose a brewery uses a Cobb-Douglas production function for his production. He studies the production process and finds the following. An additional machine-hour of fermentation capacity would increase output by 500 bottles per day (i. e. MPK = 500). An additional man-hour of labor would increase output by 1000 bottles per day (i. e. MPL = 1000). The price of a man- hour of labor is $50 per hour. The price of a machine-hour of fermentation capacity is $5 per hour. 1. Is the brewery currently minimizing its cost of production? Check using the minimization condition. 2. It turns out, the brewery is not optimally chossing the factors of production. To lower its production cost, which factor of production should the brewery increase and which factor should he decrease? 3. Suppose that the price of a machine-hour of fermentation capacity rises to $25 per hour. How does this change the answer from part 1?arrow_forwardProblem 1. Costs for Sedate Sedan, Inc. (adapted from Nicholson). Sedate Sedan, Inc. uses robots and workers to assemble automobiles. There is a diminishing rate of technical substitution between robots and labour: robots do well at tasks that are purely repetitive, while labour does better at jobs that are less boring and require more thought. The various combinations of hours of robot use (r) and hours of labour use (1) needed to assemble sedans are described by the Cobb-Douglas production function: q = f(r,l) = ²√√√² 50 Note that marginal products for this production function are given by: MP: = 1 √r MP₁ Please make sure you know how to calculate them. This production function 100 Vi exhibits diminishing marginal products: the marginal product of robots decreases when more robots are used; the marginal product of labour decreases when more labour is used. The company can rent all the robots it wants for v = 40 dollars per hour and hire all the workers it wants at w = 40 dollars per…arrow_forward
- Douglas Fur is a small manufacturer of fake-fur boots in New York City. The following table shows the company’s total cost of production at various production quantities.arrow_forwardSuppose that widgets can be produced using two different production techniques, A and B. The following table provides the total input requirements for each of five different total output levels. Q = 1 Tech. K L A 4 1 B 1 3 Total Cost Q = 2 K L 2 5 6 2 Q=1 $6 L K Q = 3 Assuming that the price of labor (PL) is $2 and the price of capital (PK) is $1, calculate the total cost of production for each of the five levels of output using the optimal (least-cost) technology at each level. K 9 4 Q = 4 L K L 4 12 7 11 8 8 5 12 7 15 To do this, complete the table below by calculating the total cost of production, filling in the missing values using the optimal (least-cost) technology at each level. (Enter your responses as whole numbers.) Q = 5 $27 Q=2 $ 10 Q = 5 K L Q = 3 $ 17 Q = 4 $ 26 How many labor hours (units of labor) would be employed at each level of output? How many machine hours (units of capital)? To answer this, complete the table below for the units of labor and units of capital that…arrow_forwardIke’s Bikes is a major manufacturer of bicycles. Currently, the company produces bikes using only one factory. However, it is considering expanding production to two or even three factories. The following table shows the company’s short-run average total cost (SRATC) each month for various levels of production if it uses one, two, or three factories. (Note: Q equals the total quantity of bikes produced by all factories.) Number of Factories Average Total Cost (Dollars per bike) Q = 100 Q = 200 Q = 300 Q = 400 Q = 500 Q = 600 1 360 200 160 240 400 720 2 540 300 160 160 300 540 3 720 400 240 160 200 360 Suppose Ike’s Bikes is currently producing 500 bikes per month in its only factory. Its short-run average total cost is per bike. Suppose Ike’s Bikes is expecting to produce 500 bikes per month for several years. In this case, in the long run, it would choose to produce bikes using . On the following graph, plot the three SRATC…arrow_forward

 Principles of Economics (12th Edition)EconomicsISBN:9780134078779Author:Karl E. Case, Ray C. Fair, Sharon E. OsterPublisher:PEARSON
Principles of Economics (12th Edition)EconomicsISBN:9780134078779Author:Karl E. Case, Ray C. Fair, Sharon E. OsterPublisher:PEARSON Engineering Economy (17th Edition)EconomicsISBN:9780134870069Author:William G. Sullivan, Elin M. Wicks, C. Patrick KoellingPublisher:PEARSON
Engineering Economy (17th Edition)EconomicsISBN:9780134870069Author:William G. Sullivan, Elin M. Wicks, C. Patrick KoellingPublisher:PEARSON Principles of Economics (MindTap Course List)EconomicsISBN:9781305585126Author:N. Gregory MankiwPublisher:Cengage Learning
Principles of Economics (MindTap Course List)EconomicsISBN:9781305585126Author:N. Gregory MankiwPublisher:Cengage Learning Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning
Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning Managerial Economics & Business Strategy (Mcgraw-...EconomicsISBN:9781259290619Author:Michael Baye, Jeff PrincePublisher:McGraw-Hill Education
Managerial Economics & Business Strategy (Mcgraw-...EconomicsISBN:9781259290619Author:Michael Baye, Jeff PrincePublisher:McGraw-Hill Education





