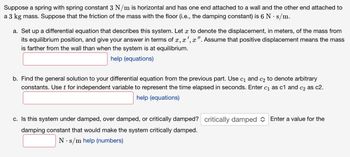
Suppose a spring with spring constant 3 N/m is horizontal and has one end attached to a wall and the other end attached to a 3 kg mass. Suppose that the friction of the mass with the floor (i.e., the damping constant) is 6 N s/m. a. Set up a differential equation that describes this system. Let x to denote the displacement, in meters, of the mass from its equilibrium position, and give your answer in terms of x, x', x". Assume that positive displacement means the mass is farther from the wall than when the system is at equilibrium. help (equations) b. Find the general solution to your differential equation from the previous part. Use c₁ and c₂ to denote arbitrary constants. Use t for independent variable to represent the time elapsed in seconds. Enter c₁ as c1 and c₂ as c2. help (equations) c. Is this system under damped, over damped, or critically damped? critically damped Enter a value for the damping constant that would make the system critically damped.

A 1.3 kg block is attached to a spring with spring constant 13 N/m. While the block is sitting at rest, a student hits it with a hammer and almost instantaneously gives it a speed of 39 cm/s. Part A: What is the amplitude of the subsequent oscillations? Part B: What is the block's speed at the point where x=0.40 A?

A mass m = 3.3 kg is at the end of a horizontal spring on a frictionless horizontal surface. The mass is oscillating with an amplitude A = 4.5 cm and a frequency f = 1.5 Hz. a. Write an equation for the spring constant k.  b. Calculate the spring constant k, in Newtons per meter.  c. Write an equation for the total mechanical energy, E, of the motion. Your expression should be in terms of the variables in the original problem statement.  d. Calculate the total mechanical energy E, in joules.

Not all "springs" are described well by Hooke's law; Hooke's law is a "first order" approximation. Say that a spring exerts a force F that is the following function of displacement: x=xi Please see the image below for the rest of the problem and answer choices.

A rubber band of mass 0.3167 g is stretched between two fingers. The overall stretched length of the band is 20.33 cm. One side of the band is plucked, setting up a vibration in 9.613 cm of the band's stretched length. The lowest frequency of vibration that can be set up on this part of the rubber band is 239.1 Hz. What is the tension in each side of the rubber band? Assume that the band stretches uniformly. N

You will solve the following problem twice, first using kinematics and second using the ideas of conservation of energy: A mass is attached to a spring with a spring constant of k=11 N/m. The motion of the mass can be described by the equation x(t) = 35 cos (1.2n t), where x(t) is cm. You want to figure out how fast the mass is moving at x = 28 cm. A. Find a solution using the kinematic relationship, v(t) = x(t). B. Find a solution using the principle of conservation of energy: E = KE + U

question d and e please For any vector quantity, be sure to always include the magnitude and direction(teacher asked)

A block with a mass m = 2.5 kg is pushed into an ideal spring whose spring constant is k = 4520 N/m. The spring is compressed x = 0.066 m and released. After losing contact with the spring, the block slides a distance of d = 2.25 m across the floor before coming to rest. a. Write an expression for the coefficient of kinetic friction between the block and the floor using the symbols given in the problem statement and g (the acceleration due to gravity). (Do not neglect the work done by friction while the block is still in contact with the spring.)

A 2 kg mass is attached to a spring having a spring constant 8 N/m. The mass is started in motion from the equilibrium position with an initial velocity 1 m/s in the upward direction and with an applied external force F(t) = sin t. Find an expression for the displacement, x, of the mass from the equilibrium position if the force due to air resistance is - 10x N Plot x against time and interpret the main features of the graph.

The analysis of a simple pendulum assumed that the mass was a particle, with no size. A realistic pendulum is a small, uniform sphere of mass M and radius R at the end of a massless string, with I being the distance from the pivot to the center of the sphere. Part A Find an expression for the period of this pendulum. Express your answer in terms of the variables M, R, L, and free fall acceleration g. T= IVE ΑΣΦ Submit Part B Request Answer Suppose M = 25 g, R = 1.0 cm, and L = 1.0 m, typical values for a real pendulum. What is the ratio Treal/Tsimple, where Treal is your expression from part A and T'simple = 2π₁/₂ Express your answer using six significant figures. Treal/Tsimple= ? IVE ΑΣΦ ?