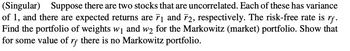
(Singular) Suppose there are two stocks that are uncorrelated. Each of these has variance of 1, and there are expected returns are 7₁ and 72, respectively. The risk-free rate is rf. Find the portfolio of weights w₁ and w₂ for the Markowitz (market) portfolio. Show that for some value of rf there is no Markowitz portfolio.

Giventwo uncorrelated stocks with variance of 1 and expected returns of r1 and r2, respectively, and a risk-free rate of rf, find the portfolio weights w1 and w2 for the Markowitz (market) portfolio. Show that for some value of rf there is no Markowitz portfolio.Defining the problem:We have two uncorrelated assets with variance 1 and expected returns $r_1$ and $r_2$, respectively.We're seeking the portfolio weights $w_1$ and $w_2$ for the Markowitz (market) portfolio, which maximizes return for a given level of risk.The optimization problem is to minimize the portfolio variance, subject to a constraint on the portfolio return.Matrix Representation:The covariance matrix for two uncorrelated assets is diagonal with variances on the diagonal, Solving the Constraints using Lagrange Multipliers:The Lagrange function is constructed using the constraints to optimize.Deriving the Lagrange function with respect to the portfolio weights and solving for them, you get expressions for portfolio that combines these assets to match the risk-free rate. This means you can't construct a portfolio with a return equal to the risk-free rate by combining these two assets in any proportion. there is no Markowitz portfolio combining these two assets to match the risk-free rate.