Question
A yo-yo is made of two uniform disks, each of mass M and radius R, which are glued to a smaller central axle of negligible mass and radius 0.5R (see figure). A string is wrapped tightly around the axle. The yo-yo is then released from rest and allowed to drop downwards, as the string unwinds without slipping from the central axle.
a) Find the moment of inertia, I, of the yo-yo with respect to an axis through the common centers of the disks, in terms of the mass and radius.
b) Calculate the magnitude of the linear velocity V, in meters per second, of the yo-yo after it has fallen a distance 0.46 m.
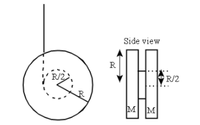
Transcribed Image Text:Side view
R
R/2
R/2
M M
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 3 images

Knowledge Booster
Similar questions
- y 11 P a aa- X If a = 4 in, determine the moment of inertia about the x-axis located at point P.arrow_forwardThe object shown below is centered on the origin, and has a width of 20 cm in the x direction, 3 cm in the y direction, and 5 cm in the z direction. Around which axis does it have the lowest moment of inertia l?arrow_forwardof Sides a and b has a mass M. Four point-like balls, each of rnass m = each corner of the plate as indicated in the figure. What is the moment of inertia of this object if the axis of M are glued to rotation is through the end of one sidt, like a door, as indicated in the figure by the blue fine? (A) Isoor=M (a² + b²) (B) Isoor= M(a² + b) (C) Idoor M(a² + b*) (D) Isoor = }M(a²+8) (F) Isoor = Ma² %3D (G) Isoor Ma? %3D (H) Idor Ma² A rectangular plate with four umall point-like balls glued to each corner. The blue line represents the axis of rotationarrow_forward
- A thin rod of mass m and length 3R connects two spheres of mass m and radius R.Find the moment of inertia of the system about the axis at the midpoint of the rod and perpendicular to it. 3R R R m marrow_forwardA space craft may be modeled as a uniform disk. Suppose the disk shaped craft has a mass of 2500 kg and a radius of 5.67 ngedalla par pplica meters. (a) What is the moment of inertia of the spacecraft? (b) Two rocket engines on opposite sides of the craft each apply an identical tangential force to impart a uniform angular acceleration in the counterclockwise sense. Suppose the craft acceleration from rest to an angular velocity of 1.00 revolutions per second in the counter clockwise sense over a period of 30.0 seconds. What is this final angular velocity in radians per second? (c) What is the angular acceleration of the craft over the period of uniform angular ac- celeration? (d) What net torque is needed to achieve the angular acceleration in part (c)? (e) What force is applied by each rocket engine during the period of uniform angular accel- eration?arrow_forwardCalculate the moment of inertia of a skater given the following information. a) The 70-kg skater is approximated as a cylinder that has a 0.144-m radius. kg m? b) The skater with arms extended is approximately a cylinder that is 50.1 kg, has a 0.144-m radius, and has two 0.973-m-long arms which are 3.92 kg each and extend straight out from the cylinder like rods rotated about their ends. kg m?arrow_forward
arrow_back_ios
arrow_forward_ios