Recall that ims that very large data digit disproportionately often. In fact, research has shown that if you randomly draw a number from a very large data file, the probability of getting a number with "1" as the leading digit is about 0.301. Now suppose you are the auditor for a very large corporation. The revenue file contains millions of numbers in a large computer data bank. You draw a random sample of n = 227 numbers from this file and r = 85 have a first nonzero digit of 1. Let p represent the population proportion of all numbers in the computer file that have a leading digit of 1. (i) Test the claim that p is more than 0.301. Use α = 0.05. (a) What is the level of significance? State the null and alternate hypotheses. OHO: P= 0.301; H₁: p > 0.301 OHO: p > 0.301; H₁: p = 0.301 OH: P = 0.301; H₂: p = 0.301 O Ho: P= 0.301; H₂: p < 0.301 (b) What sampling distribution will you use? O The standard normal, since np < 5 and nq < 5. The Student's t, since np < 5 and nq < 5. O The Student's t, since np > 5 and nq > 5. O The standard normal, since np > 5 and nq > 5. What is the value of the sample test statistic? (Round your answer to two decimal places.)
Recall that ims that very large data digit disproportionately often. In fact, research has shown that if you randomly draw a number from a very large data file, the probability of getting a number with "1" as the leading digit is about 0.301. Now suppose you are the auditor for a very large corporation. The revenue file contains millions of numbers in a large computer data bank. You draw a random sample of n = 227 numbers from this file and r = 85 have a first nonzero digit of 1. Let p represent the population proportion of all numbers in the computer file that have a leading digit of 1. (i) Test the claim that p is more than 0.301. Use α = 0.05. (a) What is the level of significance? State the null and alternate hypotheses. OHO: P= 0.301; H₁: p > 0.301 OHO: p > 0.301; H₁: p = 0.301 OH: P = 0.301; H₂: p = 0.301 O Ho: P= 0.301; H₂: p < 0.301 (b) What sampling distribution will you use? O The standard normal, since np < 5 and nq < 5. The Student's t, since np < 5 and nq < 5. O The Student's t, since np > 5 and nq > 5. O The standard normal, since np > 5 and nq > 5. What is the value of the sample test statistic? (Round your answer to two decimal places.)
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
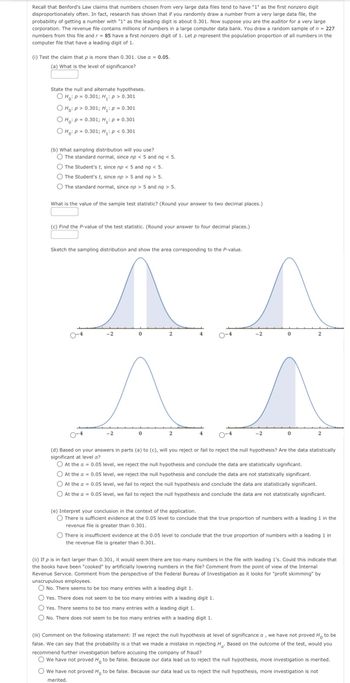
Transcribed Image Text:Recall that Benford's Law claims that numbers chosen from very large data files tend to have "1" as the first nonzero digit
disproportionately often. In fact, research has shown that if you randomly draw a number from a very large data file, the
probability of getting a number with "1" as the leading digit is about 0.301. Now suppose you are the auditor for a very large
corporation. The revenue file contains millions of numbers in a large computer data bank. You draw a random sample of n = 227
numbers from this file and r = 85 have a first nonzero digit of 1. Let p represent the population proportion of all numbers in the
computer file that have a leading digit of 1.
(i) Test the claim that p is more than 0.301. Use α = 0.05.
(a) What is the level of significance?
State the null and alternate hypotheses.
Ho: P = 0.301; H₁: p > 0.301
O Ho: P> 0.301; H₁: p = 0.301
O Ho: P= 0.301; H₁: p = 0.301
O Ho: p = 0.301; H₂: p < 0.301
(b) What sampling distribution will you use?
The standard normal, since np < 5 and nq < 5.
The Student's t, since np < 5 and nq < 5.
The Student's t, since np > 5 and nq > 5.
The standard normal, since np > 5 and nq > 5.
What is the value of the sample test statistic? (Round your answer to two decimal places.)
(c) Find the P-value of the test statistic. (Round your answer to four decimal places.)
Sketch the sampling distribution and show the area corresponding to the P-value.
-2
-2
0
2
2
4
4
-2
-2
0
0
2
2
(d) Based on your answers in parts (a) to (c), will you reject or fail to reject the null hypothesis? Are the data statistically
significant at level a?
O At the α = 0.05 level, we reject the null hypothesis and conclude the data are statistically significant.
O At the α = 0.05 level, we reject the null hypothesis and conclude the data are not statistically significant.
O At the α = 0.05 level, we fail to reject the null hypothesis and conclude the data are statistically significant.
O At the x = 0.05 level, we fail to reject the null hypothesis and conclude the data are not statistically significant.
(e) Interpret your conclusion in the context of the application.
O There is sufficient evidence at the 0.05 level to conclude that the true proportion of numbers with a leading 1 in the
revenue file is greater than 0.301.
There is insufficient evidence at the 0.05 level to conclude that the true proportion of numbers with a leading 1 in
the revenue file is greater than 0.301.
(ii) If p is in fact larger than 0.301, it would seem there are too many numbers in the file with leading 1's. Could this indicate that
the books have been "cooked" by artificially lowering numbers in the file? Comment from the point of view of the Internal
Revenue Service. Comment from the perspective of the Federal Bureau of Investigation as it looks for "profit skimming" by
unscrupulous employees.
No. There seems to be too many entries with a leading digit 1.
Yes. There does not seem to be too many entries with a leading digit 1.
O Yes. There seems to be too many entries with a leading digit 1.
O No. There does not seem to be too many entries with a leading digit 1.
(iii) Comment on the following statement: If we reject the null hypothesis at level of significance &, we have not proved Ho to be
false. We can say that the probability is a that we made a mistake in rejecting H. Based on the outcome of the test, would you
recommend further investigation before accusing the company of fraud?
We have not proved Ho to be false. Because our data lead us to reject the null hypothesis, more investigation is merited.
We have not proved Ho to be false. Because our data lead us to reject the null hypothesis, more investigation is not
merited.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step 1: Given Information:
VIEWStep 2: State the level of significance and the hypotheses:
VIEWStep 3: Identify the sampling distribution and determine the test statistic value:
VIEWStep 4: Determine the p-value and identify the appropriate normal curve:
VIEWStep 5: State and interpret the results from (a) - (c):
VIEWSolution
VIEW
Step by step
Solved in 6 steps with 31 images
Recommended textbooks for you
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON
The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman