Quarter car suspension model The figure below a model of the suspension of a car. r(t)is the position of the mass of the car from its equilibrium position while z is the profile of the road. Note that z is a function of the distance y along the road, but you need (t) which you can obtain from z(y) using the chain rule. The car is traveling to the right on the road at a speed v. Assume the mass of the car is 250 kg, the spring constant is 16 kN/m, and damping constant is 1000 Ns/m. (a) Derive the differential equation for the position of the car r(t). (b) If z(t) Zoejwot, determine the amplitude and the phase of the particular solution. (c) (MATLAB) If the car is travelling with constant velocity along a road with rolling hills that can be represented as a cosine function with amplitude Zo and wavelength A (wavelength is the distance between adjacent crests or adjacent troughs, determine the vertical motion of the car as a function of time.
Quarter car suspension model The figure below a model of the suspension of a car. r(t)is the position of the mass of the car from its equilibrium position while z is the profile of the road. Note that z is a function of the distance y along the road, but you need (t) which you can obtain from z(y) using the chain rule. The car is traveling to the right on the road at a speed v. Assume the mass of the car is 250 kg, the spring constant is 16 kN/m, and damping constant is 1000 Ns/m. (a) Derive the differential equation for the position of the car r(t). (b) If z(t) Zoejwot, determine the amplitude and the phase of the particular solution. (c) (MATLAB) If the car is travelling with constant velocity along a road with rolling hills that can be represented as a cosine function with amplitude Zo and wavelength A (wavelength is the distance between adjacent crests or adjacent troughs, determine the vertical motion of the car as a function of time.
Elements Of Electromagnetics
7th Edition
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Sadiku, Matthew N. O.
ChapterMA: Math Assessment
Section: Chapter Questions
Problem 1.1MA
Related questions
Question
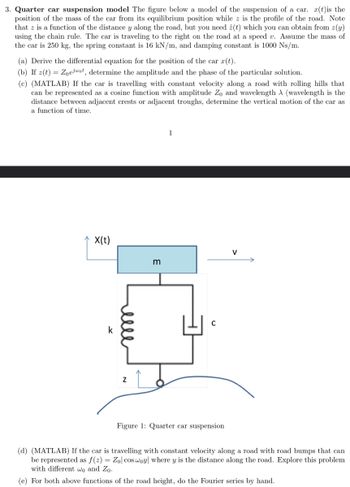
Transcribed Image Text:3. Quarter car suspension model The figure below a model of the suspension of a car. r(t)is the
position of the mass of the car from its equilibrium position while z is the profile of the road. Note
that z is a function of the distance y along the road, but you need ż(t) which you can obtain from z(y)
using the chain rule. The car is traveling to the right on the road at a speed v. Assume the mass of
the car is 250 kg, the spring constant is 16 kN/m, and damping constant is 1000 Ns/m.
(a) Derive the differential equation for the position of the car r(t).
(b) If z(t) = Zoejot, determine the amplitude and the phase of the particular solution.
(c) (MATLAB) If the car is travelling with constant velocity along a road with rolling hills that
can be represented as a cosine function with amplitude Zo and wavelength A (wavelength is the
distance between adjacent crests or adjacent troughs, determine the vertical motion of the car as
a function of time.
X(t)
Z
m
1
C
Figure 1: Quarter car suspension
(d) (MATLAB) If the car is travelling with constant velocity along a road with road bumps that can
be represented as f(z) = Zol cos woy where y is the distance along the road. Explore this problem
with different wo and Zo.
(e) For both above functions of the road height, do the Fourier series by hand.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 6 steps with 14 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you
Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education
Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:
9781118170519
Author:
Norman S. Nise
Publisher:
WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:
9781118807330
Author:
James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:
WILEY