EBK CONTEMPORARY FINANCIAL MANAGEMENT
14th Edition
ISBN: 9781337514835
Author: MOYER
Publisher: CENGAGE LEARNING - CONSIGNMENT
expand_more
expand_more
format_list_bulleted
Related questions
Question
Transcribed Image Text:Part 1: Net Present Value (NPV)
First, we need to calculate the annual cash flow. The net income is given, and since depreciation is a
non-cash expense, we add it back to net income to find the cash flow:
Annual Cash Flow = Net Income + Depreciation
Annual Cash Flow = $200,000+ $200,000
Annual Cash Flow = $400,000
The project lasts for 8 years with an initial investment of $2,000,000. The NPV formula is:
CE
NPV - Initial Investment
=
t=1
where CF, is the annual cash flow, is the discount rate, and 12 is the number of years.
NPV=
400,000
- 2,000,000
t=1 (1+0.10)
Calculating each term:
Year 1:
Year 2:
Year 3:
400,000
(1+0.10)1
400,000
(1+0.10)²
400,000
(1+0.10)
400,000
1.10
400,000
363, 636.36
330, 578.51
1.21
400,000
=
300, 525.98
1.331
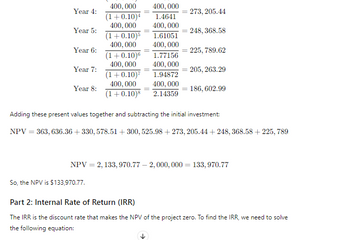
Transcribed Image Text:Year 4:
400,000 400,000
(1+0.10)4 1.4641
400,000 400,000
273, 205.44
Year 5:
248, 368.58
(1+0.10)5 1.61051
Year 6:
Year 7:
Year 8:
400,000 400,000
(1+0.10)6 1.77156
400,000 400,000
(1+0.10)7 1.94872
400,000 400,000
(1+0.10)8 2.14359
225, 789.62
=205, 263.29
= 186, 602.99
Adding these present values together and subtracting the initial investment:
NPV 363, 636.36 + 330, 578.51 +300, 525.98 +273, 205.44 + 248, 368.58 +225,789.
NPV = 2,133,970.77-2, 000, 000 = 133,970.77
So, the NPV is $133,970.77.
Part 2: Internal Rate of Return (IRR)
The IRR is the discount rate that makes the NPV of the project zero. To find the IRR, we need to solve
the following equation:
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 6 images
Knowledge Booster
Similar questions
- Foster Manufacturing is analyzing a capital investment project that is forecast to produce the following cash flows and net income: The payback period of this project will be: a. 2.5 years. b. 2.6 years. c. 3.0 years. d. 3.3 years.arrow_forwardYou've estimated the following cash flows (in $) for a project: A B 1 Year Cash flow The required return for the project is 8%. Part 1 What is the IRR for the project? 3+ decimals Submit 2 0 -5,200 3 1 1,300 4 2 2,100 5 3 4,000 2 Attempt Attemparrow_forwardConsider the following two mutually exclusive projects: Year Cash Flow (A) Cash Flow (B) -$ 15,456 5,225 8,223 13,013 8,705 0 1 234 -$ 276,363 26,400 51,000 57,000 402,000 Whichever project you choose, if any, you require a 6 percent return on your investment. a. What is the payback period for Project A? Payback period b. What is the payback period for Project B? Payback period c. What is the discounted payback period for Project A? Discounted payback periodarrow_forward
- A project will generate the following cash flows. If the required rate of return is 15%, what is the project’s net present value? Year Cash flow 0 –$50,000 1 $15,000 2 $16,000 3 $17,000 4 $18,000 5 $19,000 Select one: a. $16,790.47 b. $6,057.47 c. $3,460.47 d. $1,487.21 e. –$3,072.47arrow_forwardAn investment project requires an initial cash outlay of $800 and then generates the following cash flows. End of year 1: $200 End of year 2: $ 300 End of year 3: $500 What is the IRR of this project?arrow_forwardNeed answer with correct calculationarrow_forward
- Using the method of your choice calculate the Net Present Value of the following cash flows. Assume that the required return on this project is 15% Project A Initial Cost -$150 Year 1 $175 Yeat 2 $100arrow_forwardThe initial cost of a project is $18 million. If a project returns $3 million at year 1 and that cash flow increases by $2 million each year afterwards, what is the payback period? The initial cost of a project is $18 million. If a project returns $3 million at year 1 and that cash flow increases by $2 million each year afterwards, what is the payback period? 5.77 years 4.25 years 3.33 years 2.66 yearsarrow_forwardA project has the following cash flows. What is the payback period? Year Cash Flow 0 −$10,000 1 1,800 2 3,600 3 5,000 4 6,000arrow_forward
- At a required rate of return of 15.0%, Project B's present value is obviously higher than that of Project A. How much higher is the present value of Project B's cash flows than Project A's cash flows? Years: 0 1 2 3 Project A's Cash Flows: $0 Project B's Cash Flows: $0 A. $ 1,686 B. $ 2,949 C. $ 5,041 D. $ 7,481 E. $ 9,699 $1,000 $6,000 $2,000 $4,000 $4,000 $2,000 4 $6,000 $1,000arrow_forwardI will rate. Solve correctly and show all works.arrow_forwardThere is a project with the following cash flows : Year Cash Flow 0 −$ 23,350 1 6,300 2 7,400 3 8,450 4 7,350 5 5,900 What is the payback period?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- EBK CONTEMPORARY FINANCIAL MANAGEMENTFinanceISBN:9781337514835Author:MOYERPublisher:CENGAGE LEARNING - CONSIGNMENT
Managerial AccountingAccountingISBN:9781337912020Author:Carl Warren, Ph.d. Cma William B. TaylerPublisher:South-Western College Pub
Financial And Managerial AccountingAccountingISBN:9781337902663Author:WARREN, Carl S.Publisher:Cengage Learning, 
Intermediate Financial Management (MindTap Course...FinanceISBN:9781337395083Author:Eugene F. Brigham, Phillip R. DavesPublisher:Cengage Learning
EBK CONTEMPORARY FINANCIAL MANAGEMENT
Finance
ISBN:9781337514835
Author:MOYER
Publisher:CENGAGE LEARNING - CONSIGNMENT
Managerial Accounting
Accounting
ISBN:9781337912020
Author:Carl Warren, Ph.d. Cma William B. Tayler
Publisher:South-Western College Pub
Financial And Managerial Accounting
Accounting
ISBN:9781337902663
Author:WARREN, Carl S.
Publisher:Cengage Learning,
Intermediate Financial Management (MindTap Course...
Finance
ISBN:9781337395083
Author:Eugene F. Brigham, Phillip R. Daves
Publisher:Cengage Learning