In this problem, we will apply Gauss's law to a conducting shell that surrounds a charge. This problem is spherically symmetric, which makes it an ideal candidate for a Gauss's law analysis. A hollow conductor carries a net charge of +7 nC. In its cavity, insulated from the conductor, is a small, isolated sphere with a net charge of -5 nC. How much charge is on the outer surface of the hollow conductor? How much is on the inner surface of the cavity? 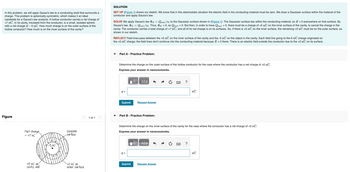Figure Net charge - +7 nC +5 nC on cavity wall Gaussian surface +2 nC on outer surface 1 of 1 > SOLUTION SET UP (Figure 1) shows our sketch. We know that in this electrostatic situation the electric field in the conducting material must be zero. We draw a Gaussian surface within the material of the conductor and apply Gauss's law. SOLVE We apply Gauss's law g = Qenel/€o to the Gaussian surface shown in (Figure 1). The Gaussian surface lies within the conducting material, so E = 0 everywhere on that surface. By Gauss's law, g = Qencl/co. Thus, g = 0, so Qencl = 0. But then, in order to have Qencl = 0, there must be a charge of +5 nC on the inner surface of the cavity, to cancel the charge in the cavity. The conductor carries a total charge of +7 nC, and all of its net charge is on its surfaces. So, if there is +5 nC on the inner surface, the remaining +2 nC must be on the outer surface, as shown in our sketch. REFLECT Field lines pass between the +5 nC on the inner surface of the cavity and the -5 nC on the object in the cavity. Each field line going to the-5 nC charge originated on the +5 nC charge; the field lines don't continue into the conducting material because E=0 there. There is an electric field outside the conductor due to the +2 nC on its surface. ▾ Part A - Practice Problem: Determine the charge on the outer surface of the hollow conductor for the case where the conductor has a net charge of +2 nC. Express your answer in nanocoulombs. ΠΫΠΙ ΑΣΦ q= Submit ▾ Part B - Practice Problem: Request Answer q= Submit → Determine the charge on the inner surface of the cavity for the case where the conductor has a net charge of +2 nC. Express your answer in nanocoulombs. [95] ΑΣΦΑ @ Request Answer C ? nC C Q ? nC

An infinitely long rod lies along the x-axis and carries a uniform linear charge density λ = 5 μC/m. A hollow cone segment of height H = 27 cm lies concentric with the x-axis. The end around the origin has a radius R1 = 8 cm and the far end has a radius R2 = 16 cm. Refer to the figure. a. Consider the conic surface to be sliced vertically into an infinite number of rings, each of radius r and infinitesimal thickness dx. Enter an expression for the electric flux differential through one of these infinitesimal rings in terms of λ, x, and the Coulomb constant k.  b. Integrate the electric flux over the length of the cone to find an expression for the total flux through the curved part of the cone (not including the top and bottom) in terms of λ, H, and the Coulomb constant k. Enter the expression you find.  c. Calculate the electric flux, in N•m2/C, through the circular end of the cone at x = 0.  d. Calculate the electric flux, in N•m2/C, through the circular end of the cone at x = H.  e.…

The first part is the question, however I'm asking for help on subpart D & E.