
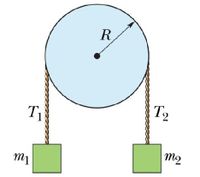
In the figure, block 1 has mass m1 = 0.460 kg, block 2 has mass m2 = 0.500 kg, and the pulley, which is mounted on a horizontal axle with negligible friction, has radius R = 0.0500 m. Tension T1, the tension force on block 1, is 4.54N. Tension T2, the tension force on block 2, is 4.87N. What is the net torque acting on the pulley?
Please note that I know that the answer is to be that taunet = -T1R + T2R
Why is tau1 = -T1R? Why is tau2 = T2R? Is the angle between R and the tension force in each case 90o? And so the formula tau = r F sin theta is simply tau = F r = T R here? What about the sign?
Here is where I need help: I do not know how to determine the signs of the torques, that is, how to determine the direction of the rotation (clockwise or counterclockwise). Please explain what is the axis of rotation here, and how to determine the direction of the rotation (clockwise or counterclockwise) for this problem specifically and in general. I know that the convention is that if the direction of rotation is counterclockwise, then the torque is positive, and if the direction is clockwise, then the torque is negative. But how do you determine the direction of the rotation?
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

- A bowl is rotating on a potter's wheel at constant angular speed as shown. The friction force between his hands and the bowl is 1.70 N total. If the bowl has a diameter of 13.0 cm, how large is the torque on the wheel? Report a positive answer.arrow_forwardA bicycle wheel, of radius 0.300 m and mass 1.16 kg (concentrated on the rim), is rotating at 4.00 rev/s. After 54.2 s the wheel comes to a stop because of friction. What is the magnitude of the average torque due to frictional forces? ____ N⋅marrow_forwardA turntable must spin at 33.3 rev/min (3.49 rad/s) to play an old-fashioned vinyl record. How much torque must the motor deliver if the turntable is to reach its final angular speed in 2.30 revolutions, starting from rest? The turntable is a uniform disk of diameter 30.5 cm and mass 0.210 kg. _____N·marrow_forward
- A bar of length 3.00 m is hinged at one end and experiences a force of 8.00 N at the other end. The torque applied is 10.0N⋅m. What must be the angle between the line of force and the extended line of the bar ϕ?arrow_forwardA 15.2 m long crane makes an angle of 25.0° with the horizontal. A 482 kg wrecking ball hangs vertically from the end of the crane. What torque does it cause about the base of the crane? Equations: Fg = mg t = Fr sinqarrow_forwardTwo blocks are connected by massless string that is wrapped around a pulley. Block 1 has a mass m1=6.00 kg, block 2 has a mass m2=2.00 kg, while the pulley has a mass of 1.00 kg and a radius of 18.0 cm. When the pulley turns, there is friction in the axel that exerts a torque of magnitude 0.410 N m. If block 1 is released from rest at a height h=1.40 m, how long does it take to drop to the floor?arrow_forward
- In the figure, block 1 has mass m1 = 0.460 kg, block 2 has mass m2 = 0.500 kg, and the pulley, which is mounted on a horizontal axle with negligible friction, has radius R = 0.0500 m. Tension T1, the tension force on block 1, is 4.54N. Tension T2, the tension force on block 2, is 4.87N. What is the net torque acting on the pulley? Please note that I know that the answer is to be that taunet = -T1R + T2R Why is the torque associated with T1 negative when it produces a counterclockwise rotation, and the torque associated with T2 positive when it produces a clockwise rotation? I thought that if the direction of rotation was counterclockwise, then the torque is positive, and if the direction was clockwise, then the torque is negative.arrow_forwardProblem 2. Three forces are applied to a disk of radius 0.35 m and mass 2.5 kg, as shown in figure below. One force is perpendicular to the rim, one is tangent to it, and the other one makes a 40.0° angle with the radius. The moment of inertia of a disk about its center is I = (1/2)MR². (a) What is the net torque on the disk due to these three forces for an axis perpendicular to the disk and passing through its center? (b) What is the angular acceleration of the disk? 11.9 N 0.350 m 40.0° 14.6 N 8.50 Narrow_forwardA wrench 30 cm long is attached to a nut and bolt. You exert a 15 N force on the wrench. What is the maximum torque you can exert under these conditions?arrow_forward
- In the figure, what magnitude of force F applied horizontally at the axle of the wheel is necessary to raise the wheel over an obstacle of height h = 0.356 m? The wheel's radius is r = 0.662 m and its mass is m = 1.71 kg. Farrow_forwardAs a torque activity, your Physics TA sets up the arrangement shown below. 3 F_= A uniform rod of mass m = 118 g and length L = 100.0 cm is attached to the wall with a pin as shown. Cords are attached to the rod at the r₁ = 10.0 cm and r₂ = 90.0 cm mark, passed over pulleys, and masses of m₁ = 271 g and m₂ = 137 g are attached. Your TA asks you to determine the following. (a) The position r3 on the rod where you would suspend a mass m3 = 200 g in order to balance the rod and keep it horizontal if released from a horizontal position. In addition, for this case, what force (magnitude and direction) does the pin exert on the rod? Use standard angle notation to determine the direction of the force the pin exerts on the rod. Express the direction of the force the pin exerts on the rod as the angle F, measured with respect to the positive x-axis (counterclockwise is positive and clockwise is negative). m4 F_= OF = "5 (b) Let's now remove the mass m3 and determine the new mass m4 you would…arrow_forwardPLEASE SEND THE ANSWER IN 10 MINUTES !!! Find the magnitude of the net torque on the wheel in Figure below about the axle through O, taking a=13cm, b=41cm. The magnitude of the applied forces are F1=11N, F2=20N, and F3=11N. Provide your answer in units of m⋅N and round off your answer to 2 decimal places.arrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





