Simple harmonic motion
Simple harmonic motion is a type of periodic motion in which an object undergoes oscillatory motion. The restoring force exerted by the object exhibiting SHM is proportional to the displacement from the equilibrium position. The force is directed towards the mean position. We see many examples of SHM around us, common ones are the motion of a pendulum, spring and vibration of strings in musical instruments, and so on.
Simple Pendulum
A simple pendulum comprises a heavy mass (called bob) attached to one end of the weightless and flexible string.
Oscillation
In Physics, oscillation means a repetitive motion that happens in a variation with respect to time. There is usually a central value, where the object would be at rest. Additionally, there are two or more positions between which the repetitive motion takes place. In mathematics, oscillations can also be described as vibrations. The most common examples of oscillation that is seen in daily lives include the alternating current (AC) or the motion of a moving pendulum.
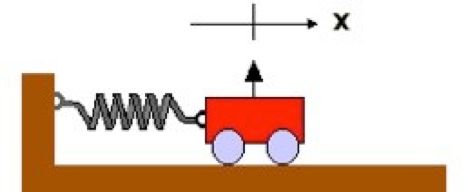
B. If the spring constant is k = 2.2 N/m, can you find the mass of the cart? If you can do it, give the answer here. If you can't, put 0.
m = _______ kg
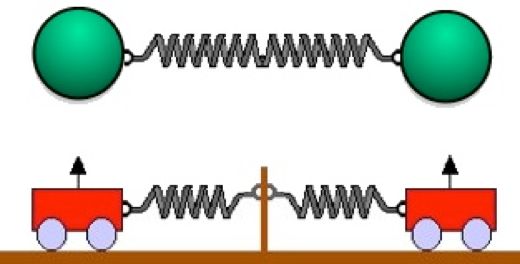
| The simple mass on a spring is the basis for our description of almost any oscillation. Lets consider the vibrational states of a simple diatomic molecule, say N2. We will model it as two identical masses connected by a spring as shown in the figure at the top right. This is a little different from the cart on a spring since there is no wall -- both of the atoms are moving. But if we only look at oscillations of the molecule where the center of mass is not moving, the atoms are moving equally and oppositely. When one is going left, the other goes an equal amount to the right and vice versa. This is like two carts attached to a wall and oscillating equally and oppositely as shown in the lower picture. The only difference is the way we treat the spring. When each atom moves a distance x, the spring between the atoms actually stretches a distance 2x, so the force on each atom is -2kx. We can therefore model the motion of one of the nitrogen atoms as a single cart on a spring if we replace k by 2k. |
C. If the angular frequency of oscillation of N2 is found to be 4.5 x 1018 rad/s, and the mass of a single nitrogen atom is 2.3 x 10-26 kg, find the effective spring constant between the two atoms. (Give your answer in N/nm, since nanometers is a more appropriate scale for atoms than meters.)
k = _______ N/nm
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images
