**Finding the Mean and Standard Deviation of Binomial Random Variables**To calculate the mean and standard deviation for each binomial random variable, follow these instructions. Ensure you round the mean to two decimal places and the standard deviation to four decimal places as needed.### Given Problems:**a.** $ n = 56 $, $ \pi = 0.95 $- **Mean:** 53.20- **Standard Deviation:** *(Input required)***b.** $ n = 95 $, $ \pi = 0.75 $- **Mean:** 71.25- **Standard Deviation:** *(Input required)***c.** $ n = 48 $, $ \pi = 0.90 $- **Mean:** 43.20- **Standard Deviation:** *(Input required)*### Instructions:1. **Calculating the Mean:** - Formula: $ \text{Mean} = n \times \pi $ - Substitute the values for $ n $ and $ \pi $ from each problem.2. **Calculating the Standard Deviation:** - Formula: $ \text{Standard Deviation} = \sqrt{n \times \pi \times (1 - \pi)} $ - Substitute the values for $ n $ and $ \pi $ from each problem. Ensure all calculations are rounded correctly as specified.

Mean and standard deviation for binomial distribution

Find the mean and standard deviation for each binomial random variable: a. n = 56, T = .95 (Round your mean value to 2 decimal places and standard deviation to 4 decimal places.) Mean 53.20 Standard deviation

Find the mean and standard deviation for each binomial random variable: a. n = 56, T = .95 (Round your mean value to 2 decimal places and standard deviation to 4 decimal places.) Mean 53.20 Standard deviation

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Q: Find the mean, variance, and standard deviation of the binomial distribution with the given values…

A: The given values are:n (number of trials) = 123p (probability of success on each trial) = 0.48

Q: Scores on a test are normally distributed with a mean of 76 and a standard deviation of 6. Using the…

Q: An electronic module used by the Navy in a sonar device requires replacement onthe average once…

A: Introduction: It is given that replacement is required for the sonar device on a particular aircraft…

Q: An insurance salesperson sells an average of 4.90 policies per day. Let x denote the number of…

Q: Most colleges here in the Philippines requires applicants for admission to take the College…

A: Consider X : scores on CAT X~Nμ=527,σ=112

Q: Find the mean and variance for the binomial distribution, P=0.37,n=22

A: Answer: From the given data, p = 0.37 and q = 1 - p = 1 - 0.37 = 0.63 sample size ( n )= 22

Q: Calculate for the mean, MAD and MAD squared using the chart below. The data set below gives the…

A: Since you have posted a question with multiple sub-parts, we will solve the first three subparts for…

Q: The monthly rents for studio have a apartments in Abu Dhabi mean of AED 3400 and a standard…

A: GivenMean(μ)=3400standard deviation(σ)=400sample size(n)=25

Q: The combined SAT scores for the students at a local high school are normally distributed with a mean…

A: Given: Mean=1487 standard deviation=307

Q: IQ scores are normally distributed with a mean of 100 and a standard deviation of 15. Find the IQ…

A: Excel formula: =NORMINV(0.305,0,1)=-0.5100

Q: The total annual precipitation for a region is approximately normally distributed with a mean of…

A: Given data normal distributionμ = 1050 mmσ = 400 mmP(1050<x<1300) = ?

Q: Cody took his first physics exam and scored an 80. The population mean for this exam is 70, and the…

A: Solution: It is given that, Population mean, 70 Standard deviation, 5 Given that Cody took his first…

Q: Find the mean and variance for the binomial distribution, P=0.56 and n= 8

A: Number of trials n=8 Success of probability p=0.56 X~binomial (n,p)

Q: 90% of all children spend at least how many hours per day unsupervised? hours.

A: We have given that. X~N( μ , ?^2 ) μ=2.9 , ? =1.3 Z-score =( x - μ )/?

Q: A study on the body mass index (BMI) reported that the distribution of the BMI is lognormal for…

A: Let X be the women aged 35-45 P(X<24.5)=?

Q: Trucks in a delivery fleet travel a mean of 130 miles per day with a standard deviation of 39 miles…

A: The data on per day mileage of a delivery truck is normally distributed. Population mean, Population…

Q: b Find the probability that the college graduate has between $15,050 and $21,200 in student loan…

A: Given Mean= 25400S Standarddeviation = 10950 Find P(15050<X<21200)=?

Q: If the standard deviation is low, the scores are close to each other O the same O far apart some are…

A: In order to get a proper idea about the overall nature of a given set of values, it is necessary to…

Q: the length of time it takes college students to find a parking spot follows a normal distribution…

A: Given, μ=5 minutesσ=1 minutes

Q: IQ scores for students at a prestigious university are normally distributed with a mean of 110 and a…

Q: Find the mean and variance for the Binomial distribution, P=0.36 and n = 33

A: Answer: From the given data, P = 0.36 and n = 33

Q: The life of light bulbs is distributed normally. The standard deviation of the lifetime is 36 hours…

A: Answer: From the given data, mean(μ) = 500 standard deviation (σ) = 36 X~ Norma(500,36) at most 508…

Q: Scores on a test are normally distributed with a mean of 76 and a standard deviation of 6. Using the…

Q: how do you find standard deviation? how many bars should you have for a standard deviation? do you…

A: Introduction:The standard deviation of a set of observations is the square root of the average of…

Q: Find the mean and variance for the binomial distribution, P=0.45 and n=12

A: Answer:- Given, Sample size, n = 12 Probability of success on a trial, p = 0.45 Using formulas,…

Q: The standard deviation is also called the give-or-take value. True

A: we have to state that the given statement is true or false. statement : The standard deviation is…

Q: SAT test scores are normally distributed with a mean of 500 and a standard deviation of 100. Find…

A: Given: Let X be the SAT test scores Mean(X)=500 SD(X)=100 X~ Normal(500, 1002)

Q: Scores on a math test are normally distributed with a mean of 76 and a standard deviation of 6. Part…

A: Let, X=the scores on a math test Given that X follows a normal distribution with mean=76 and…

Q: A normal population has mean u = 55 and standard deviation o = 9. What is the 84th percentile of the…

A: Given that mean u = 55 and standard deviation o = 9.

Q: Calculate the expected value, the variance, and the standard deviation of the given random variable…

Q: Mean, Variance, Standard deviation, & Z-scores for each set. N=5 (5, 7, 7, 5, 5) (7, 7, 11, 7, 10)

A: The observations in set 1 are 5, 7, 7, 5, 5 that is number of observations N = 5 Mean = x = sum of…

Q: A statistics professor gives a survey to each of the 100 students in an introductory statistics…

A: Obtain the population standard deviation:

Q: Finding the Mean, Variance, and Standard Deviation of a Binomial Distribution About 9% of the…

A: Solution : Given : n = 100 p = 0.09 q = 1- p = 0.91For Binomial…

Q: Solve the problem. Assume that mountain lions' weights are normally distributed with a mean of 62.6…

A: We have given that, X be the random variable from normal distribution with mean (μ) = 62.6 ,…

Q: The number of tickets purchased by an individual for Beckham Colleges holiday music festival is a…

A: Let X denotes the number of tickets purchased by an individual for Beckham Colleges holiday music…

Q: Medicare Hospital Insurance The average yearly Medicare Hospital Insurance benefit per person was…

A: Given that. X~N( μ , ?) μ=4064 , ?=460 Z-score =( x - μ )/?

Q: Trucks in a delivery fleet travel a mean of 100 miles per day with a standard deviation of 38 miles…

Q: Find the mean, variance, and standard deviation of the binomial distribution with the given values…

A: In this problem, we are given the following values:n (number of trials) = 123p (probability of…

Concept explainers

Continuous Probability Distributions

Probability distributions are of two types, which are continuous probability distributions and discrete probability distributions. A continuous probability distribution contains an infinite number of values. For example, if time is infinite: you could count from 0 to a trillion seconds, billion seconds, so on indefinitely. A discrete probability distribution consists of only a countable set of possible values.

Normal Distribution

Suppose we had to design a bathroom weighing scale, how would we decide what should be the range of the weighing machine? Would we take the highest recorded human weight in history and use that as the upper limit for our weighing scale? This may not be a great idea as the sensitivity of the scale would get reduced if the range is too large. At the same time, if we keep the upper limit too low, it may not be usable for a large percentage of the population!

Question

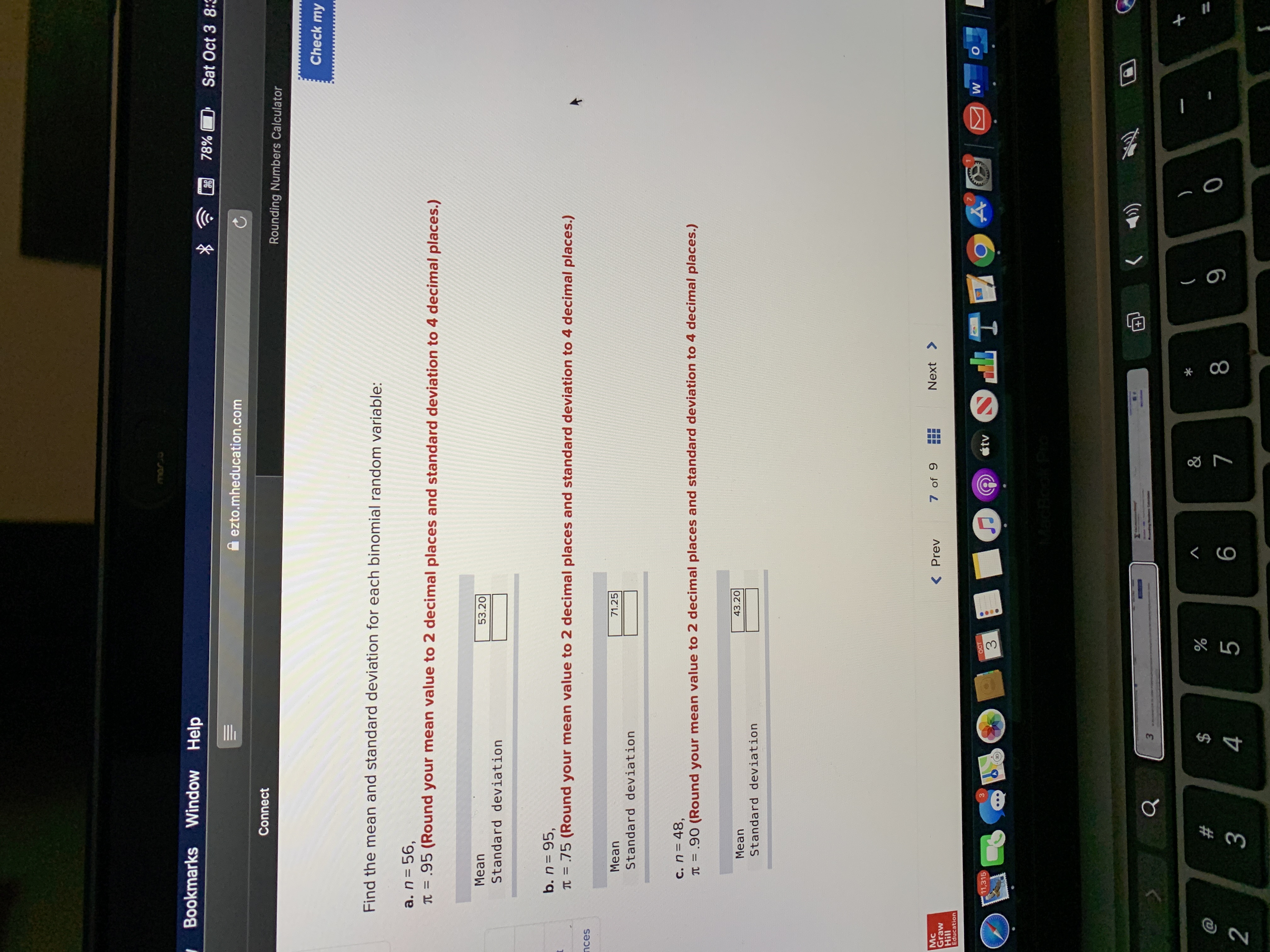
**Finding the Mean and Standard Deviation of Binomial Random Variables**

To calculate the mean and standard deviation for each binomial random variable, follow these instructions. Ensure you round the mean to two decimal places and the standard deviation to four decimal places as needed.

### Given Problems:

**a.** $ n = 56 $, $ \pi = 0.95 $

- **Mean:** 53.20
- **Standard Deviation:** *(Input required)*

**b.** $ n = 95 $, $ \pi = 0.75 $

- **Mean:** 71.25
- **Standard Deviation:** *(Input required)*

**c.** $ n = 48 $, $ \pi = 0.90 $

- **Mean:** 43.20
- **Standard Deviation:** *(Input required)*

### Instructions:
1. **Calculating the Mean:**
- Formula: $ \text{Mean} = n \times \pi $
- Substitute the values for $ n $ and $ \pi $ from each problem.

2. **Calculating the Standard Deviation:**
- Formula: $ \text{Standard Deviation} = \sqrt{n \times \pi \times (1 - \pi)} $
- Substitute the values for $ n $ and $ \pi $ from each problem.

Ensure all calculations are rounded correctly as specified.

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

This is a popular solution!

SEE SOLUTION Check out a sample Q&A here

Step 1

VIEW

Step 2

VIEW

Step 3

VIEW

Trending now

This is a popular solution!

Step by step

Solved in 3 steps with 11 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Continuous Probability Distribution$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions

SAT : MEAN IS 500 STANDARD DEVIATION IS 100 ACT: MEAN IS 20 STANDARD DEVIATION IS 6
Calculate the expected value, the variance, and the standard deviation of the given random variable X. (Round all answers to two decimal places.) X is the number of red marbles that Suzan has in her hand after she selects four marbles from a bag containing four red marbles and two green ones. expected value variance standard deviation Need Help? Read It
Please show the complete solution. Thanks!
Cody took his first physics exam and scored an 80. The population mean for this exam is 70, and the standard deviation is 5. What is the probability of selecting a person with a score greater than Cody’s?
Repair Cost for Microwave Ovens The average repair cost of a microwave oven is $55, with a standard deviation of $8. The costs are normally distributed. Find the probability that the mean of the repair bills will be greater than $70.
Find the mean and standard deviation for each Poisson: a. A = 6 (Round your standard deviation to 3 decimal places.) Mean Standard deviation b. A = 18 (Round your standard deviation to 3 decimal places.) Mean Standard deviation c. A = 3 (Round your standard deviation to 3 decimal places.) Mean Standard deviation
Españiol A scientist has read that the mean birth weight of babies born at full term is 7.4 pounds. The scientist has good reason to believe that the mean birth weight of babies born at full term, µ, is different from this value and plans to perform a statistical test. She selects a random sample of birth weights of babies born at full term and finds the mean of the sample to be 7.8 pounds and the standard deviation to be 1.8 pounds. Based on this information, complete the parts below. (a) What are the null hypothesis H. and the alternative hypothesis H, that should be used for the test? Ho :0 O
An electrical firm manufactures incandescent light bulbs that have a length of life (in hours) that is normally distributed. If the mean and standard deviation length of life of all lightbulbs produced are 1250 hours and 300 hours respectively, find the probability that a randomly selected bulb will last less than 1100 hours. Do NOT round off until you arrive at the FINAL ANSWER. Round off final answer to 3 decimal places example: (1.234)
Round z-score to the nearest hundredth and then find the required A values using the table. The amount of time customers spend waiting in line at a bank normally distributed, with a mean of 3.0 minutes and a standard deviation of 7.5 minute. Find the probability that the time a customer spends waiting is as follows. (A) Less than 3.5 minutes and (B) less than 1.5 minutes.
Find the variance and standard deviation. Round the variance to two decimal places and standard deviation to at least three decimal places.
z Scores LeBron James, one of the most successful basketball players of all time, has a height of 6 feet 8 inches, or 203 cm. Based on statistics from Data Set 1 “Body Data” in Appendix B, his height converts to the z score of 4.07. How many standard deviations is his height above the mean?
A flooring company sells carpet by the metre off of a standard sized roll. The mean amount of carpet sold per month is known to have a normal distribution. If the probability of selling more than 1,000 metres per month is 0.0668 and the standard deviation is 100 metres, what is the mean amount of carpet sold? 900 1100 1150 850 The amount of coffee poured into a large coffee cup at the campus Tim Horton's has a distribution that is skewed to the right with a mean of 600 ml and a standard deviation of 50 ml. For a random sample of 100 large cups poured, what is the mean of the sampling distribution? 50 600 100 50 √100