
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Consider the map T : R3 → R3 given by T(x, y, z) = (x − 2y + z ,−3y + 2z, − x − y + z)
Choose only one answer as correct.
(a) The matrix of this linear transformation in the base β = {(1, 0, 0),(0, 1, 0),(0, 0, 1)} is given by (image)
(b) T is a one-to-one linear transformation which is equivalent to saying that Ker(T)={(0, 0, 0)}.
(c) T is a surjective linear transformation, since the image of T, Im(T), has dimension 3. Thus, Im(T) = R3.
(d) T is a linear transformation whose kernel, Ker(T), is a 1-dimensional
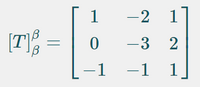
Transcribed Image Text:1
-2 1
-3 2
L-1
-1
1
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Consider the linear transformation T: R3 R defined by T(x, y, z) = (x – 3y + 2z, 3x + y + 5z, -2x + 6y – 4z). Find the standard matrix of T.arrow_forwardLet T be the linear transformation defined by T(x, y) = (-9y,4x + y, 5y – 8x, 2y – 7x). Find its associated matrix A. A =arrow_forwardLet T: R R' be a linear transformation such that T(1, 0, 0) - (2, -1, 4), T(0, 1, 0) = (1, -2, 3), and T(0, 0, 1) = (-2, 0, 2). Find the indicated image. T(1, -4, 2) T(1, -4, 2) - (-10,18, – 6)arrow_forward
- Find the matrix of the linear transformation T from R2 - R² where T([1, 0]) = [1, –2] and T([2, 1]) = [2, 3] %3D (Note: matrix A = [T([1, 0]), T([0, 1])] 1 -2 (a) 1 (b) 1 (c) -2 (d) -2 3 7 3 Ob a Carrow_forwardSuppose T is a linear transformation on R² (i.e. T(x, y) = (ax + by, cx + dy) where a, b, c, d are real numbers and, interpreting T as a matrix, det(T) # 0. Let P be the parallelogram which is the image of the square D = = [0, 1] × [0, 1] (i.e. T(D) =P). Then the area of P is given by O lad - bcl ad bc abcd 1 |ad - bc| O labcd|arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

