
Database System Concepts
7th Edition
ISBN: 9780078022159
Author: Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
Consider the case of Alice sending a message, m, to Bob.
Both Alice and Bob use public key cryptography and each has a public and private key as described in the text. The figure attached below shows the operations that Alice must perform to provide confidentiality, authentication, and integrity when sending a message to Bob over the network.
We can use either symmetric key or public key cryptography to encrypt a message. For our purposes, either technique will encrypt the message, and applying both doesn't make it "more secure". Also, we can assume that the session key would remain a secret so the fact that it is discarded does not make it "more secure". Why do we use a session key, Ks, instead of relying only on public key Cryptography? In other words, why do we use both public key and symmetric key cryptography?
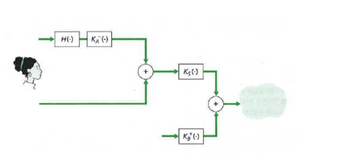
Transcribed Image Text:H(-)
KA (•)
Ks(-)
Kg (-)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- Explain this more What is the tradeoff however with each pass? Answer here: Minimum 200 words addressing tradeoffs. I’m understanding this question, in the way that if we apply ciphers multiple times using the same key then it will either completely negate encryption an even number of encryptions attempts or only apply it once for an odd number of encryption attempts. If we have a secure password, then we can focus on protocols and systems instead of passwordsarrow_forwardNow assume that the user used only 34 characters from the keyboard. What is the key length in bits in this case? Provide the correct answer for the fourth question. This is not a graded assignment.arrow_forwardNote: The notation from this problem is from Understanding Cryptography by Paar and Pelzi. Consider the LFSR represented by the polynomial x¹ + x³ +x+1 What are the tap bits of the LFSR? Please enter your answer as unspaced binary digits (e.g. 010101 to represent p = 0, P4 = 1, P3 = 0, P2 = 1, P₁ = 0, Po = 1).arrow_forward
- A secure email system is expected to provide confidentiality, sender's non-repudiation, and message integrity. Alice uses three keys to achieve this goal. The three keys are Alice's private key (KA), Bob's public key (Kg), and a randomly generated symmetric key (Ks). The encryption procedure is shown below: How can Bob 1) decrypt the data, 2) verify the message's integrity, and 3) verify the sender's non-repudiation? Describe the detailed steps (including the formulas) and show your work. KA m H(-) KA( m I am using SHA-256 KA(H(M)) Ks() KB(*) K Ks K.(m, KA(H(m)) + + KB(Ks) Internet 34arrow_forwardI need help with the following problems in cryptography. A. Encrypt the message “Freedom” using the Playfair matrix M F H I K U N O P Q Z V W X Y E L A R G D S T B C T B. Construct the Playfair matrix with the keyword “LARGEST” and encrypt the message “Freedom” again. C. Compare the results obtained in A and B. How do you account for these results?arrow_forward. Q: There is no authentication in the Diffie-Hellman key-exchange protocol. By exploiting this property, a malicious third party, Chuck, can easily break into the key exchange taking place between Alice and Bob, and subsequently ruin the security. Explain how this would work.arrow_forward
- The definition of a Shift Cipher can be expressed as follows:Def. Let x, y, k ∈ Z26 with the encryption operation as ek(x) ≡ x + k mod 26 and thedecryption operation as dk(y) ≡ y - k mod 26.Given the provided letter encoding, what would be the encoding of the plaintext word ATTACKafter applying a shift cipher with a k=17?arrow_forwardIn this problem we explore the relationship between password length and cryptographic security. Suppose a password consists of 77 ASCII characters. You can review the ASCII characters here.. Exactly 27=12827=128 of these codes are for printable characters; we will assume every character in the password is printable. What is the size of the keyspace that consists of passwords of this form?What is the equivalent key length in bits? Assuming that you could check one password every 10−810−8 seconds, what is the worst case running time for cracking this password by brute force search (in days)? Now assume that the user used only 3131 characters from the keyboard. What is the key length in bits in this case? How many days, in the worst case, would it take to break this weaker password? You can't round to the nearest day here -- be as exact as possible. Supposing you used only 3131 characters, how long is the shortest password that achieves 252252 bits of security?arrow_forwardThe notation from this problem is from Understanding Cryptography by Paar and Pelzl. Consider the LFSR represented by the polynomial x^4+x^3+x+1. What are the tap bits of the LFSR? Please enter your answer as unspaced binary digits (e.g. 010101 to represent p5=0,p4=1,p3=0,p2=1,p1=0,p0=1arrow_forward
- Alice and Bod have decided to use a symmetric encryption algorithm. They have some assumptions about their messages:- Messages only contain capital letters (i.e. A to Z)- The length of their shared key must be greater than or equal to the length of the plaintext- They assign each letter a number as follows: (A,0), (B,1), (C,2), (D,3),…, (Z,25)Their algorithm combines the key and the message using modular addition. The numerical values of corresponding message and key letters are added together, modulo 26. For example, if the plain text is “HELLO” and the key is “SECRET” then the encrypted message is calculated as following:Since the length of the plaintext is 5, we just need the first 5 letters of the key (i.e. “SECRE”), then for each letter, we should add corresponding letters in both the plaintext and the key modulo 26.Plaintext: H (7) E (4) L (11) L (11) O (14)Key: S (18) E (4) C (2) R (17) E(4)Cipher: Z (25) I (8) N(13) C(2) S (18) Write a program in Python, C/C++ or JavaScript to…arrow_forwardEach of the following is a true/false statement about a tweakable block cipher (TBC). Place a checkmark next to each true statement. In the questions mentioning E', let E' be a random instance of a TBC and E'(T,X) be the result of using E' with tweak T and input X. Group of answer choices: (1)For TBC security both the current key and tweak in use must be kept secret from adversaries. (2)Each time a new tweak is given to a TBC, the TBC behaves like a new random permutation. (3)When a TBC is used once per tweak its outputs may be considered (4)A TBC is a prominent part of the design of OCB. (5)If X1 ≠ X2, then always E'(T,X1) ≠ E'(T,X2) (6)If T1 ≠ T2, then always E'(T1,X) ≠ E'(T2,X)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education

Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON

C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON

Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning

Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education