MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Topic Video
Question
thumb_up100%
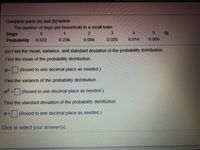
Transcribed Image Text:**Probability Distribution of Dogs per Household**
The following details a probability distribution for the number of dogs per household in a small town:
| Dogs | Probability |
|------|-------------|
| 0 | 0.622 |
| 1 | 0.236 |
| 2 | 0.094 |
| 3 | 0.026 |
| 4 | 0.014 |
| 5 | 0.008 |
**Tasks:**
(a) *Calculate the Mean, Variance, and Standard Deviation of the Probability Distribution.*
- **Mean (μ):** Compute the expected value by multiplying each number of dogs by its probability and summing the results.
\(\mu = \sum (x \cdot P(x))\)
\(\mu = \boxed{\ } \) (Round to one decimal place as needed.)
- **Variance (\(\sigma^2\)):** Compute the variance by finding the expected value of the squared deviations from the mean.
\(\sigma^2 = \sum ((x - \mu)^2 \cdot P(x))\)
\(\sigma^2 = \boxed{\ } \) (Round to one decimal place as needed.)
- **Standard Deviation (\(\sigma\)):** The standard deviation is the square root of the variance.
\(\sigma = \boxed{\ } \) (Round to one decimal place as needed.)
*Click to select your answer(s).*
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 3 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- The histogram shows the reviewer ratings on a scale from 1 (lowest) to 5 (highest) of a recently published book. Reviewer Ratings 0.5- 0.4- 0.3- 0.2- 0.14 0.022 0.01 0.444 (a) Find the mean, variance, and standard deviation of the probability distribution. (b) Interpret the results. 0.249 0.214 0.071 Rating (a) The mean is (Type an integer or a decimal. Do not round.) The variance is. (Round to two decimal places as needed.) The standard deviation is (Round to two decimal places as needed.) (b) Interpret the results. Select all that apply. O A. The typical rating deviates from the mean by about 4. O B. The average rating for the book is approximately 4. O C. The typical rating deviates from the mean by about 1. O D. The average rating for the book is approximately 1. Probabilityarrow_forwardComplete parts (a) and (b) below. The number of dogs per household in a small town Dogs 0 2 Probability 0.638 0.089 1 0.223 0= 3 0.026 4 0.015 5 0.008 (a) Find the mean, variance, and standard deviation of the probability distribution. Find the mean of the probability distribution. (Round to one decimal place as needed.) Find the variance of the probability distribution. o² = (Round to one decimal place as needed.) Find the standard deviation of the probability distribution. (Round to one decimal place as needed.) (b) Interpret the results in the context of the real-life situation. A. A household on average has 0.6 dog with a standard deviation of 15 dogs. B. A household on average has 1.0 dog with a standard deviation of 0.6 dog. C. A household on average has 0.9 dog with a standard deviation of 1.0 dog. OD. A household on average has 0.6 dog with a standard deviation of 1.0 dog. 0arrow_forwardK← Complete parts (a) and (b) below. The number of dogs per household in a small town Dogs 0 2 Probability 0.663 0.083 1 0.214 3 0.020 4 0.014 5 0.006 (a) Find the mean, variance, and standard deviation of the probability distribution. Find the mean of the probability distribution. μ= (Round to one decimal place as needed.)arrow_forward
- Save Use the probability distribution to complete parts (a) and (b) below. The number of defects per 1000 machine parts inspected Defects 1 4 Probability 0.262 0.301 0.243 0.138 0.042 0.014 (a) Find the mean, variance, and standard deviation of the probability distribution. The mean is . (Round to one decimal place as needed.) Incorrectarrow_forwardUse the probability distribution to complete parts (a) and (b) below. The number of defects per 1000 machine parts inspected Defects 1 2 4 Probability 0.264 0.290 0.240 0.148 0.042 0.016 ..... (a) Find the mean, variance, and standard deviation of the probability distribution.arrow_forwardComplete parts (a) and (b) below. The number of dogs per household in a small town Dogs 2 0 0.630 Probability 0.090 1 0.234 3 0.022 4 0.015 5 0.009 (a) Find the mean, variance, and standard deviation of the probability distribution. Find the mean of the probability distribution. μ = (Round to one decimal place as needed.) Find the variance of the probability distribution. o² = (Round to one decimal place as needed.) Find the standard deviation of the probability distribution. (Round to one decimal place as needed.) (b) Interpret the results in the context of the real-life situation. OA. A household on average has 1.0 dog with a standard deviation of 0.6 dog. OB. A household on average has 0.6 dog with a standard deviation of 16 dogs. OC. A household on average has 0.9 dog with a standard deviation of 1.0 dog. D. A household on average has 0.6 dog with a standard deviation of 1.0 dog.arrow_forward
- Use the probability distribution to complete parts (a) and (b) below. The number of school-related extracurricular activities per student Activities 0 1 2 3 4 5 6 7 Probability 0.061 0.122 0.164 0.178 0.211 0.127 0.082 0.055 (a) Find the mean, variance, and standard deviation of the probability distribution. (b) Interpret the results. The mean is ______so the average student is involved in_____The standard deviation is_____so the typical number of activities per student deviates_______arrow_forwardFind the variance of thefollowing probability distribution. X P(X) 1 0.30 2 0.15 3 0.05 4 0.25 5 0.25 A.1.73 B.1.61 C.2.60 D.1.27arrow_forwardComplete parts (a) and (b) below. The number of dogs per household in a small town Dogs 1 3 4 Probability 0.680 0.200 0.076 0.022 0.014 0.007 .... (a) Find the mean, variance, and standard deviation of the probability distribution. Find the mean of the probability distribution. (Round to one decimal place as needed.) Help Me Solve This View an Example Get More Help-arrow_forward
- Complete parts (a) and (b) below. The number of dogs per household in a small town Dogs 3 4 5 Probability 0.644 0.220 0.089 0.023 0.015 0.009 (a) Find the mean, variance, and standard deviation of the probability distribution. Find the mean of the probability distribution. με (Round to one decimal place as needed.)arrow_forwardComplete parts (a) and (b) below. The number of dogs per household in a small town Dogs Probability 1 3 4 0.649 0.222 0.088 0.022 0.014 0.006 (a) Find the mean, variance, and standard deviation of the probability distribution. Find the mean of the probability distribution. u= (Round to one decimal place as needed.) Find the variance of the probability distribution. o = ' (Round to one decimal place as needed ) Find the standard deviation of the probability distribution. (Round to one decimal place as needed.) (b) Interpret the results in the context of the real-life situation O A. A household on average has 0.5 dog with a standard deviation of 11 dogs. O B. A household on average has 0.6 dog with a standard deviation of 0.9 dog. C. A household on average has 0.8 dog with a standard deviation of 0.9 dog. O D. A household on average has 0.9 dog with a standard deviation of 0.5 dog.arrow_forwardComplete parts (a) and (b) below. The number of dogs per household in a small town 2 4 Dogs Probability 0.674 0.206 0.079 0.022 0.013 0.007 (a) Find the mean, variance, and standard deviation of the probability distribution. Find the mean of the probability distribution. (Round to one decimal place as needed.) Find the variance of the probability distribution. o = (Round to one decimal place as needed.) Find the standard deviation of the probability distribution. (Round to one decimal place as needed.) (b) Interpret the results in the context of the real-life situation. O A. A household on average has 0.5 dog with a standard deviation of 15 dogs. OB. A household on average has 0.5 dog with a standard deviation of 0.9 dog. O C. A household on average has 0.8 dog with a standard deviation of 0.9 dog. O D. A household on average has 0.9 dog with a standard deviation of 0.5 dog. esc E1 000 F2arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning 
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman