Class Median Age Midpoint, x Income, / 15-24 years 19.5 $10,869 25-34 years 29.5 $34,113 35-44 years 39.5 $45,225 45-54 years 49.5 $46,466 55-64 years 59.5 $42,176 65 years and older 69.5 $27,612

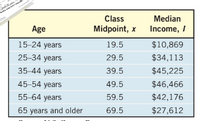
An individual’s income varies with his or her age. The following table shows the median income I of males of different age groups within the United States for 2012. For each age group, let the class midpoint represent the
independent variable, x. For the class “65 years and older,” we will assume that the class midpoint is 69.5.

(a) Use a graphing utility to draw a scatter diagram of the
data. Comment on the type of relation that may exist
between the two variables.
(b) Use a graphing utility to find the quadratic function of
best fit that models the relation between age and median
income.
(c) Use the function found in part (b) to determine the age at
which an individual can expect to earn the most income.
(d) Use the function found in part (b) to predict the peak
income earned.
(e) With a graphing utility, graph the quadratic function of
best fit on the scatter diagram.