ates. A one unit increase in magnitude represents ground shaking ten times as strong (an earthquake with magnitude 4 is ten times as strong as an earthquake with magnitude 3). Complete parts (a) through (d) below. Click the icon to view the data on earthquakes. nd the mean, median, range, standard deviation, and quartiles for both the depth and magnitude of the earthquakes. Based on the values of the mean, median, and quartiles conjecture the shape of the distribution for depth and magnit h: u = km; M= km; Range =O km; o = km; Q, = km; Q, =N km integers or decimals rounded to two decimal places as needed.) O Data on Earthquakes depth 2.23 1.76 magnitude 0.57 depth 2.5 2.57 magnitude 0.82 0.93 depth 1.83 45.22 magnitude 0.59 3.39 depth 9.42 9.58 magnitude full data set 1.57 0.99 0.97 1.09 7.46 1.52 2.51 19.93 18.52 6.59 1.59 6.06 2.22 0.9 0.52 0.01 6.51 1.17 5.11 1.38 0.35 1.35 10.86 17.3 19.87 2.34 1.56 1.11 0.68 2.09 1.16 2.71 14.17 1.4 9.39 8.05 1.62 0.87 6.37 349.12 0.76 5.02 0.75 0.8 2.39 15.68 8.58 16.53 3.02 74.9 1.92 2.39 8.79 0.63 1.59 1.5 1.8 6.44 1.79 1.03 1.14 5.13 8.5 2.25 0.19 0.66 1.13 0.39 138.21 5.86 4.27 0.56 514.99 4.29 1.39 3.06 2.69 1.92 1.71 131.46 7.36 2.4 0.75 4.9 8.15 0.84 0.47 0.35 6.82 13.13 10.87 0.1 1.97 0.43 0.99 2.41 5.84 128.65 2.19 3.29 1.33 1.99 2.51 7.03 2.88 0.89 0.9 1.62 33.77 21.37 1.33 1.59 18.52 7.24 15.92 1.58 12.21 1.07 1.02 2.08 1.03 34.94 10.07 4.62 5.5 1.1 210.77 2.88 1.9 10.86 35 0.03 2 1.29 22.66 6.96 1.27 48.34 114.39 23.22 4.36 4.28 0.05 1.19 1.3 1.17 1.7 10.7 14.87 16.32 1.42 1.07 1.11 1.4 1.28 2.6 9.59 8.49 17.21 6.28 0.93 0.89 2.27 6.44 0.62 6.37 4.71
ates. A one unit increase in magnitude represents ground shaking ten times as strong (an earthquake with magnitude 4 is ten times as strong as an earthquake with magnitude 3). Complete parts (a) through (d) below. Click the icon to view the data on earthquakes. nd the mean, median, range, standard deviation, and quartiles for both the depth and magnitude of the earthquakes. Based on the values of the mean, median, and quartiles conjecture the shape of the distribution for depth and magnit h: u = km; M= km; Range =O km; o = km; Q, = km; Q, =N km integers or decimals rounded to two decimal places as needed.) O Data on Earthquakes depth 2.23 1.76 magnitude 0.57 depth 2.5 2.57 magnitude 0.82 0.93 depth 1.83 45.22 magnitude 0.59 3.39 depth 9.42 9.58 magnitude full data set 1.57 0.99 0.97 1.09 7.46 1.52 2.51 19.93 18.52 6.59 1.59 6.06 2.22 0.9 0.52 0.01 6.51 1.17 5.11 1.38 0.35 1.35 10.86 17.3 19.87 2.34 1.56 1.11 0.68 2.09 1.16 2.71 14.17 1.4 9.39 8.05 1.62 0.87 6.37 349.12 0.76 5.02 0.75 0.8 2.39 15.68 8.58 16.53 3.02 74.9 1.92 2.39 8.79 0.63 1.59 1.5 1.8 6.44 1.79 1.03 1.14 5.13 8.5 2.25 0.19 0.66 1.13 0.39 138.21 5.86 4.27 0.56 514.99 4.29 1.39 3.06 2.69 1.92 1.71 131.46 7.36 2.4 0.75 4.9 8.15 0.84 0.47 0.35 6.82 13.13 10.87 0.1 1.97 0.43 0.99 2.41 5.84 128.65 2.19 3.29 1.33 1.99 2.51 7.03 2.88 0.89 0.9 1.62 33.77 21.37 1.33 1.59 18.52 7.24 15.92 1.58 12.21 1.07 1.02 2.08 1.03 34.94 10.07 4.62 5.5 1.1 210.77 2.88 1.9 10.86 35 0.03 2 1.29 22.66 6.96 1.27 48.34 114.39 23.22 4.36 4.28 0.05 1.19 1.3 1.17 1.7 10.7 14.87 16.32 1.42 1.07 1.11 1.4 1.28 2.6 9.59 8.49 17.21 6.28 0.93 0.89 2.27 6.44 0.62 6.37 4.71
Algebra: Structure And Method, Book 1
(REV)00th Edition
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Chapter9: Systems Of Linear Equations
Section9.6: Wind And Water Current Problems
Problem 9P
Related questions
Concept explainers
Inverse Normal Distribution
The method used for finding the corresponding z-critical value in a normal distribution using the known probability is said to be an inverse normal distribution. The inverse normal distribution is a continuous probability distribution with a family of two parameters.
Mean, Median, Mode
It is a descriptive summary of a data set. It can be defined by using some of the measures. The central tendencies do not provide information regarding individual data from the dataset. However, they give a summary of the data set. The central tendency or measure of central tendency is a central or typical value for a probability distribution.
Z-Scores
A z-score is a unit of measurement used in statistics to describe the position of a raw score in terms of its distance from the mean, measured with reference to standard deviation from the mean. Z-scores are useful in statistics because they allow comparison between two scores that belong to different normal distributions.
Topic Video
Question
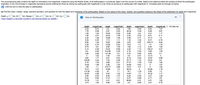
Transcribed Image Text:The accompanying data contains the depth (in kilometers) and magnitude, measured using the Richter Scale, of all earthquakes in a particular region over the course of a week. Depth is the distance below the surface at which the earthquake
originates. A one unit increase in magnitude represents ground shaking ten times as strong (an earthquake with magnitude 4 is ten times as strong as an earthquake with magnitude 3). Complete parts (a) through (d) below.
Click the icon to view the data on earthquakes.
(a) Find the mean, median, range, standard deviation, and quartiles for both the depth and magnitude of the earthquakes. Based on the values of the mean, median, and quartiles conjecture the shape of the distribution for depth and magnitude.
Depth: µ =
km; Range = km; o =
km; Q, =
km; Q3
(Type integers or decimals rounded to two decimal places as needed.)
km; M =
km
%3D
Data on Earthquakes
depth
2.23
magnitude
0.57
depth
2.5
magnitude
0.82
depth
magnitude
0.59
magnitude
1.57
depth
full data set
1.83
9.42
1.76
0.99
2.57
0.93
45.22
3.39
9.58
0.97
1.09
1.52
19.93
6.59
6.06
0.9
0.01
1.17
7.46
2.51
18.52
1.59
2.22
0.52
6.51
5.11
2.34
1.38
10.86
1.56
2.09
2.71
14.17
1.4
9.39
17.3
1.11
0.68
0.35
1.16
1.62
6.37
0.76
8.05
1.35
19.87
3.02
0.87
349.12
5.02
2.39
0.75
15.68
0.63
74.9
1.5
1.8
1.79
8.79
0.8
8.58
1.59
1.92
1.14
6.44
1.03
5.13
2.39
16.53
0.66
2.25
1.13
138.21
4.27
8.5
0.56
514.99
4.29
0.19
0.39
5.86
1.39
3.06
2.69
131.46
2.4
0.75
0.84
6.82
0.1
13.13
10.87
1.92
7.36
1.97
4.9
0.47
5.84
1.71
2.51
0.43
8.15
0.35
0.89
128.65
3.29
7.03
0.99
33.77
1.33
18.52
0.9
2.19
1.33
2.88
2.41
21.37
1.59
7.24
1.62
15.92
1.99
2.08
1.03
34.94
4.62
1.07
1.58
1.1
210.77
2.88
10.07
5.5
1.02
12.21
1.27
10.86
1.9
48.34
2
22.66
1.19
114.39
4.36
35
1.7
10.7
1.29
6.96
1.3
23.22
4.28
0.03
1.42
14.87
1.4
16.32
1.17
9.59
0.05
8.49
1.07
6.28
0.93
2.27
1.28
6.44
0.62
17.21
1.11
6.37
0.89
4.71
2.6
14.76
1.31
3.41
0.61
98.82
3.41
4.51
1.55
3.74
1.64
6.96
1.35
4.2
0.68
2.61
0.79
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Recommended textbooks for you
Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill
Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL