aram 10 20 30 40 50 cm

A mass hanging from a vertical spring is somewhat more complicated than a mass attached to a horizontal spring because the gravitational force acts along the direction of motion. Therefore, the restoring force of the oscillations is not provided by the spring force alone, but by the net force resulting from both the spring force and the gravitational force. Ultimately, however, the physical quantities of motion (position, velocity, and acceleration) for a vertical mass on a spring exhibit the same oscillations as a horizontal mass on a spring.

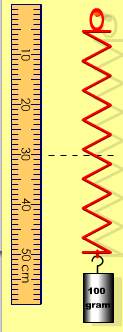
A 100 g mass hangs from a vertical spring as shown in the picture. The measuring stick shows us the vertical y position of the bottom of the spring with the origin (y = 0) at the top of the spring. Note that the positive y direction is downward. The 100 g mass is at rest at the position shown (y = 50 cm). The dashed line in the picture (y = 30 cm) indicates the unstretched resting length of the spring. The mass is pulled down 6 cm, stretching the bottom of the spring to y = 56 cm, and then released so that it begins oscillating.

Draw a free body diagram for the mass when it's at the highest point of its oscillation.
What direction is the net force on the mass at this point? If there is no net force, select No direction.  ---Select--- Down Up No direction (force is 0)

Use your free body diagram and Newton's second law to find the magnitude of the acceleration that the mass experiences at the highest point of its oscillation (this is the maximum acceleration).
|a_max| =  _______ cm/s²