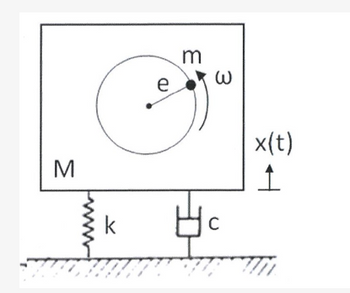
A rotating machine of 400 kg is similar to the system shown below. It operates at 3600 rpm (note: 1 rpm = 2π/60 rad/s). The machine is unbalanced such that its effect is equivalent to a 4 kg mass located 20 cm from the axis of rotation. An isolator with a spring stiffness of 8x106 N/m and a damping constant of 2x104 Ns/m is placed between the machine and the foundation. Determine the steady state response of the system. Find the force transmitted to the foundation and transmissibility of the isolator. Find the damping ratio of the system ζ . Find the transmissibility of the system, Tf. Find the frequency ratio of the system, β. Find the amplitude of the harmonic excitation force of the system, Fo in Newton (N). Find the displacement amplitude of the steady state response of the system, X in millimeters (mm). Find the damped frequency of the system, ωd in rad/s. Find the force transmitted to the foundation, FT in Newton (N). Find the frequency of the harmonic excitation of the system, ω in rad/s. Find the natural frequency of the system, ωn in rad/s. Find the natural frequency of the system, ωn in rad/s.

Consider the double mass/double spring system shown below. - click to expand. Both springs have spring constants k, and both masses have mass m; each spring is subject to a damping force of F friction We can write the resulting system of second-order DEs as a first-order system, w'(t) = Aw(t), with w = (x₁, x₁, x₂, x₂) T For values of k = 4, m = 1 and c = 21,2 = 0.5±3.2i, V₁ 23,4= - 0.5 ± 1.13i, V3 1, the resulting eigenvalues and eigenvectors of A are -0.039 0.248i 0.813 0.024 +0.153i -0.502 -0.134-0.302i' 0.409 -0.216 - 0.489i 0.661 and (a) Find a set of initial displacements x₁(0), x₂(0) that will lead to the fast mode of oscillation for this sytem. Assume that the initial velocities wil be zero. (x₁(0), x₂(0)) Enter your answer using angle braces, (and ). cx (friction proportional to velocity). (b) At what frequency will the masses be oscillating in this mode? Frequency = rad/s

Q3/ For the system shown in figure if the damping ratio is 0.3 derive the equation of motion using Newton's second law and find: a- The natural frequency. b- The damping constant. c- The ratio of any consecutive cycles. k=2 x 10 N/m m = 4.2 kg 10 cm 40 cm 60 cm ITTTI

A vehicle weighing 5,000 lb is supported on four identical springs and four identical viscous dampers. The static deflection of the vehicle under its own weight is 10 in. Determine the damping required for each of the dampers so that the critical damping is achieved.

The damping ratio of the system below is 0.3. How long will it take for the amplitude of free oscillation to be reduced to 2% of its initial value? k = 2x 10°3 N/m m = 4.2 kg 10 cm 40 cm 60 cm

A machine of mass 112.7 kg is mounted on four parallel springs each of stiffness 3.2 x 105 N/m. When the machine operates at 58.0 Hz, the machine's steady state amplitude is measured as 0.5 mm. What is the magnitude of force transmitted to the foundations of the machine at this speed? The damping in the system is negligible. (Express answers to 3sf) Answer: 3.49

The quarter-car model of a vehicle suspension and its free body diagram are shown in Figure 1. In this simplified model, the masses of the wheel, tire, and axle are neglected, and the mass m represents one-fourth of the vehicle mass. The spring constant k models the elasticity of both the tire and the suspension spring. The damping constant c models the shock absorber. The equilibrium position of m when y=0 is x=0. The road surface displacement y(t) can be derived from the road surface profile and the car’s speed. Draw free body diagram (FBD) and derive the equation of motion of m with y(t) as the input, and obtain the transfer function. If assume: m=300 kg k=20000, 40000, 60000 N/m c=1000, 3000, 5000 N.s/m Plot magnification ratio vs frequency ratio (r=0-4) diagrams for the parameters given above (you can draw the three curves in one diagram for three different k values and do the same for the three c values as well). Use the derived transfer function to model the system and plot…

a lot of people say this is the answer but some say it is not , please check for me

For a mass-spring oscillator, Newton's second law implies that the position y(t) of the mass is governed by the second-order differential equation my''(t) +by' (t) + ky(t) = 0. (a) Find the equation of motion for the vibrating spring with damping if m= 20 kg, b = 80 kg/sec, k = 260 kg/sec², y(0) = 0.3 m, and y'(0) = -0.3 m/sec. (b) After how many seconds will the mass in part (a) first cross the equilibrium point? (c) Find the frequency of oscillation for the spring system of part (a). (d) The corresponding undamped system has a frequency of oscillation of approximately 0.574 cycles per second. What effect does the damping have on the frequency of oscillation? What other effects does it have on the solution? (a) y(t) = plz answer a-d

4 QUESTION 20 The car bridge in Figure Q20 can be modelled as a damped-spring oscillator system with mass M = 10000 kg, spring coefficient k = 50000 N-m-1 and damping constant c = 50000 N-s-m-1. Cars cross the bridge in a periodic manner such that the bridge experiences a vertical force F (N) expressed by F = mg sin(10t) where m = 1136 kg is the average mass of passing cars, g = 9.81 m-s-2 is the gravitational acceleration and t (s) is the time. Determine the maximum force magnitude transmitted to the foundation (see Figure Q20) during the steady-state oscillatory response of the system. Provide only the numerical value (in Newtons) to zero decimal places and do not include the units in the answer box. E m M foundation Figure Q20: Vibrating car bridge.