Question
A pendulum swings back and forth from a string. When it is lying motionless it is y=6 ft from a nearby wall. When the pendulum is furthest from the wall, it is 9 ft. It takes 20 seconds to complete one cycle. Suppose you start timing the pendulum when it is furthest from the wall.
a) Sketch a graph of this situation.
b) Write an equation of this sinusoidal.
Expert Solution
arrow_forward
Step 1
The diagram which represents above problem is shown in the fig below:
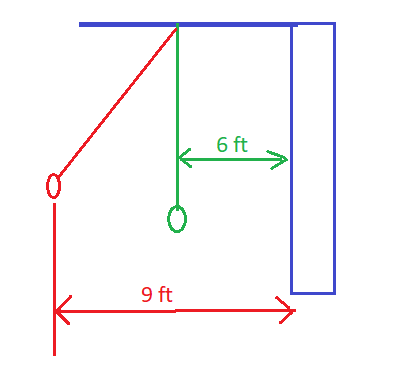
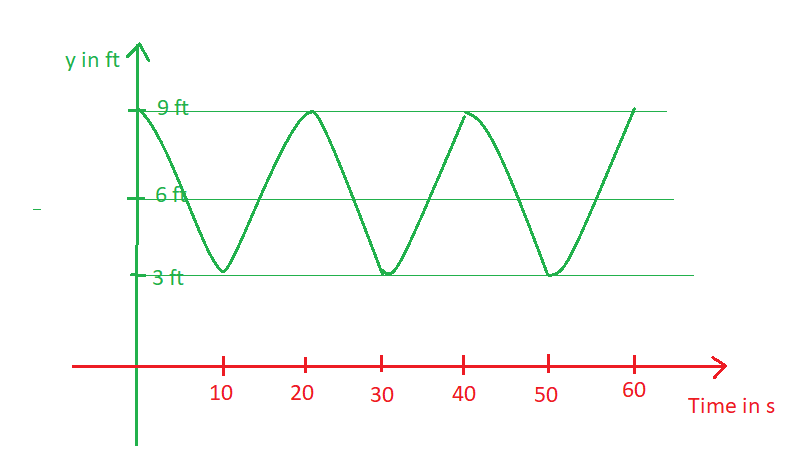
At the mean position, y=6 ft, and at the extreme position y=9 ft. So that the amplitude of the motion is 3 ft. Also given that the time period of the motion is 20 s. The graph of this oscillation is shown below:
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Near the top of the Citigroup Center building in New York City, there is an object with mass of 3.2 × 105 kg on springs that have adjustable force constants. Its function is to dampen wind-driven oscillations of the building by oscillating at the same frequency as the building is being driven—the driving force is transferred to the object, which oscillates instead of the entire building. A. What effective spring constant should the springs have to make them oscillate with a period of 2.2 s in N/m? B. What energy is stored in the springs for a 1.4 m displacement from equilibrium in J?arrow_forwardA mass of 0.407 kilograms is oscillating horizontally on a spring. Its position is given by the equation x = [0.108 sin (9.24t + 0.82) + 0.683] m. a. What is the spring constant of the spring? Include units in your answer. More information. b. The velocity of the mass is another sinusoid, which also can be modeled using the equation v = [A sin (Bt + C) + D] m/s. What are those values? Do not bother with units.A: B: C: (between 0 and 2?)D: c. The acceleration of the mass is yet another sinusoid, which again can be modeled using the equation a = [A sin (Bt + C) + D] m/s/s. What are those values of A and C? Do not bother with units. Hint: For A, consider Newton's second law of motion.A: C: (between 0 and 2?)Note that the values of B and D for the acceleration equation are the same as the values of B and D for the velocity equation.arrow_forwardQuestions 6-13 refer to the figure below. The graph represents the position as a function of time for a small 1.20 kg object attached to a light spring that is oscillating on a smooth horizontal surface. n 0.4 Time (s) 0 0.2 6. What is the amplitude of the motion (in cm)? 7. What is the period of the motion (in s)? 8. What is the frequency of the motion (in Hz)? 9. What is the angular frequency of the motion (in rad/s)? 0.6 11. What is the maximum speed of the object (in m/s)? 10. What is the spring constant of the spring (in N/m)? (Be aware of units!) 0.8 12. What is the maximum acceleration of the object (in m/s²)? 13. If instead of attaching the 1.20 kg mass to the spring, we attach a mass of 2.4 kg. What is the new period (in s) of the motion?arrow_forward
- A mass m = 3.3 kg is at the end of a horizontal spring on a frictionless horizontal surface. The mass is oscillating with an amplitude A = 4.5 cm and a frequency f = 1.5 Hz. a. Write an equation for the spring constant k. b. Calculate the spring constant k, in Newtons per meter. c. Write an equation for the total mechanical energy, E, of the motion. Your expression should be in terms of the variables in the original problem statement. d. Calculate the total mechanical energy E, in joules.arrow_forward4. The displacement y(t) of an undamped oscillator of mass m>0 on a spring with spring constant k>0, and initial displacement a + 0 and initial velocity zero satisfies my" + ky = 0, y(0) = a, y'(0) = 0 %3D a. Solve this initial value problem. b. Show that the solution is periodic with period T, meaning that y(t+T)= y(t), and express Tin terms of m and k.arrow_forward1. A pendulum with mass 2kg, length 2.5m swings with amplitude A = 2cm. After a long time the amplitude decreases to 1 cm due to air drag. How long is the period after the amplitude decrease? 2. What is the period of oscillation of the pendulum before and after the amplitude change?arrow_forward
- A pendulum makes 12 complete cycles in 20 s. What is the length of this pendulum? Select one: a. 50cm b. 60cm с. 30cm d. 40cm e. 70cmarrow_forwardQ3, first three partsarrow_forward5. A "seconds pendulum" is one that moves through its equilibrium position once each second. (The period of the pendulum is precisely 2 s.) The length of a seconds pendulum is 0.992 7 m at Tokyo, Japan and 0.994 2 m at Cambridge, England. What is the ratio of the free-fall accelerations at these two locations?arrow_forward
- 8.1arrow_forwardA 7.2 kg-block attached to a 32 N/m-spring constant spring moves on a frictionless horizontal surface, back and forth between -3.0 m and +3.0 m. What is the period of this motion, in seconds? Your answer needs to have 2 significant figures, including the negative sign in your answer if needed. Do not include the positive sign if the answer is positive. No unit is needed in your answer, it is already given in the question statement.arrow_forwardA spring with spring constant 15 N/m hangs from the ceiling. A ball is attached to the spring and allowed to come to rest. It is then pulled down 9.5 cm and released. The ball makes 20 oscillations in 23 s seconds. You may want to review (Pages 403-404) Part A What is its the mass of the ball? Express your answer to two significant figures and include the appropriate units. m = Submit Part B "i Vmax= μA Submit Value Request Answer What is its maximum speed? Express your answer to two significant figures and include the appropriate units. μA Value Units Request Answer ? Units ?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios