Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
![**Linear Transformations and Matrix Representations**
8. For each of the linear transformations below, write the matrix of the linear transformation.
a. \( T: \vec{x} \in \mathbb{R}^3 \rightarrow T(\vec{x}) \in \mathbb{R}^3 \), where \( T \) is given by:
\[
T \left( \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \right) =
\begin{bmatrix}
2x_1 - 4x_2 \\
x_1 - x_3 \\
-x_2 + 3x_3 \\
3x_1 - 2x_2
\end{bmatrix}
\]
b. \( T: \vec{x} \in \mathbb{R}^2 \rightarrow T(\vec{x}) \in \mathbb{R}^3 \), where \( T \) is given by:
\[
T \left( \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \right) =
\begin{bmatrix}
x_1 + 4x_2 \\
x_2
\end{bmatrix}
\]
c. Consider a polynomial in \( P_2 \) given by \( p(t) = a_0 + a_1 t + a_2 t^2 \). Define a linear operator \( T \) by \( T(p(t)) = (2t^2 - t + 6)p(t) \) in \( P_4 \). Find the matrix of the transformation. [Hint: See Example 2.]
d. Consider a polynomial in \( P_3 \) given by \( p(t) = a_0 + a_1 t + a_2 t^2 + a_3 t^3 \). Find the matrix of the linear transformation taking this vector into \( P_2 \) defined by the derivative operator \( \frac{d}{dt}[p(t)] \).
e. Consider the function defined as \( y(x) = a_1 e^x + a_2 e^{-x} + a_3 e^{5x} + a_4 e^{-7x} \). Write the matrix of the linear transformation defined by the derivative operator \( \frac](https://content.bartleby.com/qna-images/question/410816ed-4be2-4291-b0fb-4c8f4b2206ab/8879fd53-eee4-41ec-903b-1ab7d23c5967/y78i8b_processed.jpeg)
Transcribed Image Text:**Linear Transformations and Matrix Representations**
8. For each of the linear transformations below, write the matrix of the linear transformation.
a. \( T: \vec{x} \in \mathbb{R}^3 \rightarrow T(\vec{x}) \in \mathbb{R}^3 \), where \( T \) is given by:
\[
T \left( \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \right) =
\begin{bmatrix}
2x_1 - 4x_2 \\
x_1 - x_3 \\
-x_2 + 3x_3 \\
3x_1 - 2x_2
\end{bmatrix}
\]
b. \( T: \vec{x} \in \mathbb{R}^2 \rightarrow T(\vec{x}) \in \mathbb{R}^3 \), where \( T \) is given by:
\[
T \left( \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \right) =
\begin{bmatrix}
x_1 + 4x_2 \\
x_2
\end{bmatrix}
\]
c. Consider a polynomial in \( P_2 \) given by \( p(t) = a_0 + a_1 t + a_2 t^2 \). Define a linear operator \( T \) by \( T(p(t)) = (2t^2 - t + 6)p(t) \) in \( P_4 \). Find the matrix of the transformation. [Hint: See Example 2.]
d. Consider a polynomial in \( P_3 \) given by \( p(t) = a_0 + a_1 t + a_2 t^2 + a_3 t^3 \). Find the matrix of the linear transformation taking this vector into \( P_2 \) defined by the derivative operator \( \frac{d}{dt}[p(t)] \).
e. Consider the function defined as \( y(x) = a_1 e^x + a_2 e^{-x} + a_3 e^{5x} + a_4 e^{-7x} \). Write the matrix of the linear transformation defined by the derivative operator \( \frac
Expert Solution
arrow_forward
Step 1
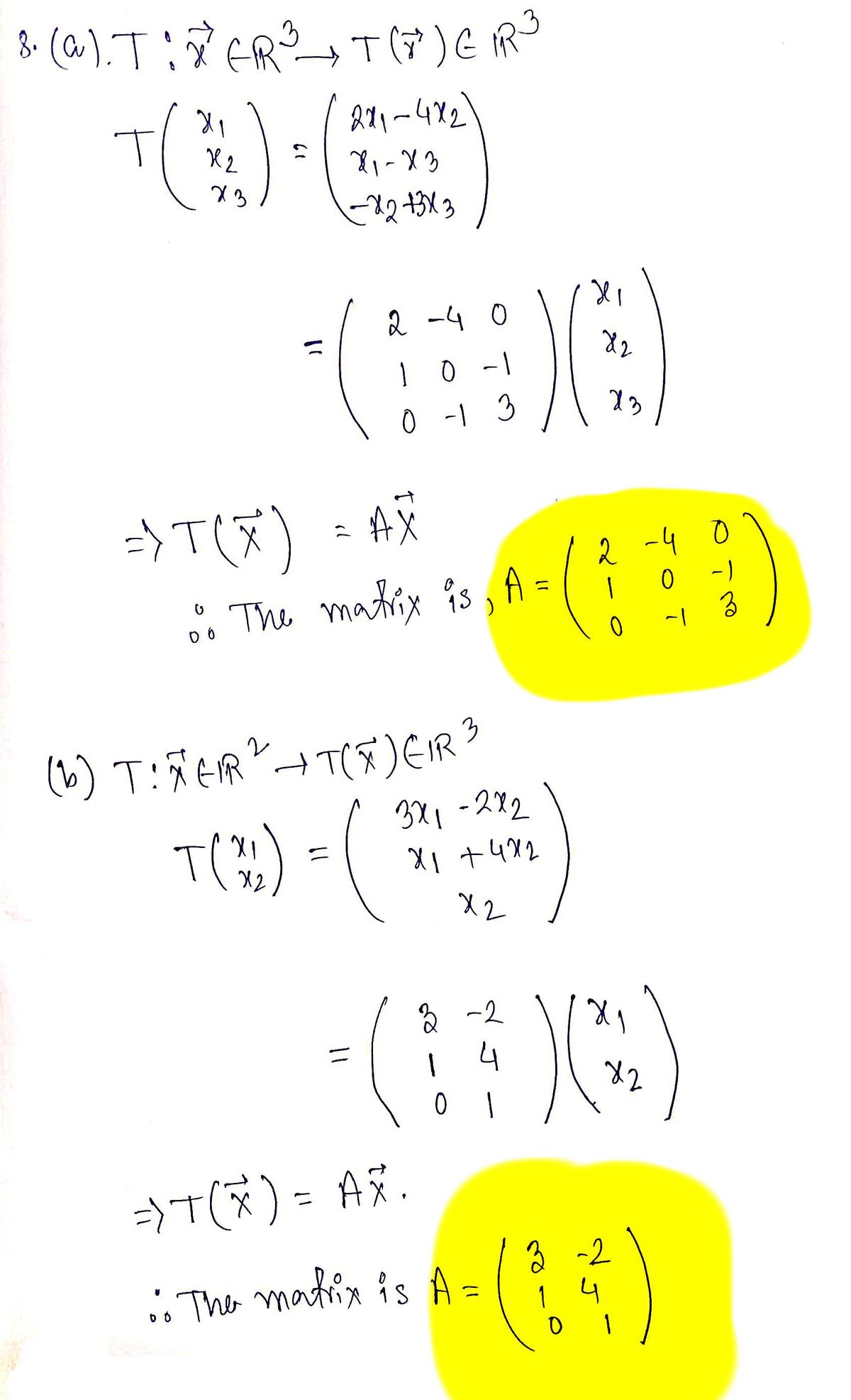
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Similar questions
- Find the standard matrix for the transformation T defined by the formula.arrow_forwardFind the matrix M of the linear transformation T: R² R² given by [H 9x1 + 3x₂ 671-7₂ T M =arrow_forwardAssume that T is a linear transformation. Find the standard matrix of T. T: R² →R² first reflects points through the vertical X2-axis and then reflects points through the horizontal x₁-axis. A = (Type an integer or simplified fraction for each matrix element.)arrow_forward
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,