6. Linear Momentum. Water flows out of a nozzle as a horizontal cylindrical jet of area Aj=0.002 m² and strikes a vertical plate. A manometer, open at the top, is connected to a small hole in the plate at the jet centerline and fills with water. The upstream area of the nozzle at section1 is A₁ = 0.01m², and the upstream gage pressure inside the nozzle, Pg1 = 2 kPa. Find: (a) the jet speed, V₁; (b) the horizontal force, Rx, that is required to hold the plate in place (coordinates shown); (c) the manometer water height, h. Ans OM: (a) Vj: 10° m/s; (b) R₂: -10° N; (c) h: 10.¹ m (¹) V₁, Pg,, Ai Az = A₂ Sha
The Laws of Physics are written for a Lagrangian system, a well-defined system which we follow around – we will refer to this as a control system (CSys). For our engineering problems we are more interested in an Eulerian system where we have a fixed control volume, CV, (like a pipe or a room) and matter can flow into or out of the CV. We previously derived the material or substantial derivative which is the differential transformation for properties which are functions of x,y,z, t. We now introduce the Reynold’s Transport Theorem (RTT) which gives the transformation for a macroscopic finite size CV. At any instant in time the material inside a control volume can be identified as a control System and we could then follow this System as it leaves the control volume and flows along streamlines by a Lagrangian analysis. RTT:DBsys/Dt = ∂/∂t ʃCV (ρb dVol) + ʃCS ρbV•n dA;
uses the RTT to apply the laws for conservation of mass, momentum (Newton's Law), and energy (1st Law of
(steady state - single pipe). The head losses are due to viscous friction effects; for ideal, inviscid flows hL = 0.
Bernoulli Eq’n (EB), as : ∆ (P/ρg + V2/2g + z) = +/- hS - hL . The shaft head work hS ≡ WS/(mg) is + for work in (pumps) and for work out (turbines). The 2nd Law of Thermodynamics requires that the viscous loss head hL is always > 0.
For SSSP CV problems, conservation of mass and momentum, m = ρVA = constant [mass flow rate, kg/s], and ∑F = m ( Vout - Vin) . While V is a scalar (speed) in the mass and EB eqns, V is a vector in the SSSP momentum CV eqn. assume adiabatic flow, neglect viscous effects, assume all units are SI consistent; Take Patm = 105 Pa ; ρwater ~ 1000 kg/m3 ; ρair ~ 1.2 kg/m3 ; g = 9.8 m/s2 ; Indicate CVs clearly
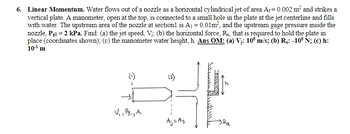
Given:
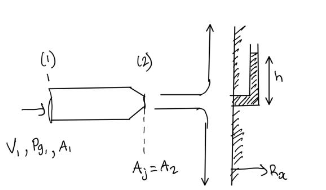
To find;
Step by step
Solved in 4 steps with 1 images
