
CALCULUS+ITS APPLICATIONS
12th Edition
ISBN: 9780135164884
Author: BITTINGER
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter R.7, Problem 2E
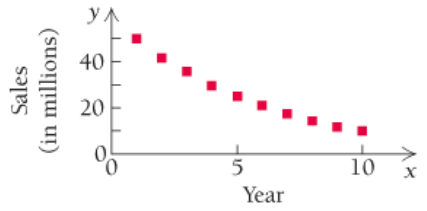
For the
Linear, f(x)=mx+b
Quadratic, f(x)=ax2+bx+c, a>0
Quadratic f(x)=ax2+bx+c, a<0
Polynomial, neither quadratic nor linear
Exponential, f(x)=a0⋅ax, 0<a or a>1 or a>1
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
=
5 37
A 4 8 0.5
06
9
Consider the following system of equations, Ax=b :
x+2y+3z - w = 2
2x4z2w = 3
-x+6y+17z7w = 0
-9x-2y+13z7w = -14
a. Find the solution to the system. Write it as a parametric equation. You can use a
computer to do the row reduction.
b. What is a geometric description of the solution? Explain how you know.
c. Write the solution in vector form?
d. What is the solution to the homogeneous system, Ax=0?
2. Find a matrix A with the following qualities
a. A is 3 x 3.
b. The matrix A is not lower triangular and is not upper triangular.
c. At least one value in each row is not a 1, 2,-1, -2, or 0
d. A is invertible.
Chapter R Solutions
CALCULUS+ITS APPLICATIONS
Ch. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - Prob. 2ECh. R.1 - Prob. 3ECh. R.1 - Prob. 4ECh. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - Prob. 7ECh. R.1 - Prob. 8ECh. R.1 - Prob. 9ECh. R.1 - In Exercises 1-22, graph each equation. Use a...
Ch. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - Prob. 13ECh. R.1 - Prob. 14ECh. R.1 - Prob. 15ECh. R.1 - Prob. 16ECh. R.1 - Prob. 17ECh. R.1 - Prob. 18ECh. R.1 - Prob. 19ECh. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - In Exercises 1-22, graph each equation. Use a...Ch. R.1 - Medicine. Ibuprofen is a medication used to...Ch. R.1 - Running records. According to at least one study,...Ch. R.1 - Optimum solar panel angle. The optimum angle A, in...Ch. R.1 - Rise in sea level. The rise in sea level t years...Ch. R.1 - Prob. 27ECh. R.1 - Use the model N=0.0011t2+0.0412t+3.032, where t is...Ch. R.1 - Snowboarding in the half-pipe. Shaun White, The...Ch. R.1 - Prob. 30ECh. R.1 - Compound interest. Southside Investments purchases...Ch. R.1 - Prob. 32ECh. R.1 - Compound interest. Stateside Brokers deposit...Ch. R.1 - Compound interest. The Kims deposit $1000 in Wiles...Ch. R.1 - Determining monthly loan payments. If P dollars...Ch. R.1 - Determining monthly loan payments. If P dollars...Ch. R.1 - Annuities. If P dollars are invested annually in...Ch. R.1 - Annuities. If P dollars are invested annually in...Ch. R.1 - Unemployment rate. The unemployment rate in the...Ch. R.1 - Prob. 40ECh. R.1 - Annual yield. The annual interest rate r, when...Ch. R.1 - Prob. 44ECh. R.1 - Prob. 45ECh. R.1 - Annual yield. The annual interest rate r, when...Ch. R.1 - Prob. 47ECh. R.1 - Chris is considering two savings accounts: Sierra...Ch. R.1 - Prob. 49ECh. R.1 - Prob. 50ECh. R.1 - Prob. 51ECh. R.1 - The Technology Connection heading indicates...Ch. R.2 - Note: A review of algebra can be found in Appendix...Ch. R.2 - Note: A review of algebra can be found in Appendix...Ch. R.2 - Note: A review of algebra can be found in Appendix...Ch. R.2 - Note: A review of algebra can be found in Appendix...Ch. R.2 - Note: A review of algebra can be found in Appendix...Ch. R.2 - Note: A review of algebra can be found in Appendix...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - Determine whether each of the following is a...Ch. R.2 - 19. A function f is given by
.
This function...Ch. R.2 - A function f is given by f(x)=3x+2 This function...Ch. R.2 - A function g is given by g(x)=x23. Find...Ch. R.2 - A function g is given by g(x)=x2+4. Find...Ch. R.2 - A function f is given by f(x)=1(x+3)2. Find...Ch. R.2 - A function f is given by f(x)=1(x5)2. This...Ch. R.2 - A function f takes a number x, multiples it by 4,...Ch. R.2 - A function g takes a number x, multiples it by 3,...Ch. R.2 - 27. A function h takes a number x. squares it, and...Ch. R.2 - 28. A function k takes a number x, squares it, and...Ch. R.2 - Graph each function. f(x)=2x5Ch. R.2 - Graph each function. f(x)=3x1Ch. R.2 - Graph each function.
31.
Ch. R.2 - Graph each function.
32.
Ch. R.2 - Graph each function.
33.
Ch. R.2 - Graph each function.
34.
Ch. R.2 - Graph each function. f(x)=6x2Ch. R.2 - Graph each function. g(x)=x2+1Ch. R.2 - Graph each function.
37.
Ch. R.2 - Graph each function.
38.
Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - Use the vertical-line test to determine whether...Ch. R.2 - In Exercises 57 and 58, assume that x is the input...Ch. R.2 - In Exercises 57 and 58, assume that x is the input...Ch. R.2 - 55. For , find .
Ch. R.2 - 56. For , and .
Ch. R.2 - For Exercises 57-60, Consider the function f given...Ch. R.2 - For Exercises 57-60, Consider the function f given...Ch. R.2 - For Exercises 57-60, Consider the function f given...Ch. R.2 - For Exercises 57-60, Consider the function f given...Ch. R.2 - Graph. f(x)={1,forx0,1,forx0Ch. R.2 - Graph.
62.
Ch. R.2 - Graph. f(x)={6,forx3,6,forx=2,Ch. R.2 - Graph. f(x)={5,forx=1,x3,forx=1,Ch. R.2 - Graph.
65.
Ch. R.2 - Graph.
66.
Ch. R.2 - Graph.
67.
Ch. R.2 - Graph.
68.
Ch. R.2 - Graph. f(x)={7,forx=2,x23,forx2Ch. R.2 - Graph. f(x)={6,forx=3,x2+5,forx3Ch. R.2 - The amount of money, A(t), in a savings account...Ch. R.2 - The amount of money, A(t), in a savings account...Ch. R.2 - Prob. 77ECh. R.2 - Prob. 78ECh. R.2 - Scaling stress factors. In psychology a process...Ch. R.2 - Solve for y in terms of x, and determine if the...Ch. R.2 - Solve for y in terms of x, and determine if the...Ch. R.2 - Solve for y in terms of x, and determine if the...Ch. R.2 - Solve for y in terms of x, and determine if the...Ch. R.2 - Explain why the vertical-line test works.Ch. R.2 - Prob. 86ECh. R.2 - In Exercises 82 and 83, use the table feature to...Ch. R.2 - In Exercises 82 and 83, use the table feature to...Ch. R.2 - 86. A function f takes a number x, adds 2, and...Ch. R.2 - 87. A function f takes a number x, adds 2, and...Ch. R.2 -
89. A function f takes a number x, multiplies it...Ch. R.2 - Prob. 94ECh. R.3 - Prob. 1ECh. R.3 - Prob. 2ECh. R.3 - Prob. 3ECh. R.3 - Prob. 4ECh. R.3 - Prob. 5ECh. R.3 - Prob. 6ECh. R.3 - Prob. 7ECh. R.3 - Prob. 8ECh. R.3 - Prob. 9ECh. R.3 - In Exercises 1-10, write interval notation for...Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Write interval notation for each of the following....Ch. R.3 - Prob. 20ECh. R.3 - In Exercises 21 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 – 32, each graph is that of a...Ch. R.3 - In Exercises 21 32, each graph is that of a...Ch. R.3 - Write the domain of each function given below in...Ch. R.3 - Write the domain of each function given below in...Ch. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 36ECh. R.3 - Prob. 37ECh. R.3 - Prob. 38ECh. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 40ECh. R.3 - Prob. 41ECh. R.3 - Prob. 42ECh. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 44ECh. R.3 - Write the domain of each function given below in...Ch. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 47ECh. R.3 - Prob. 48ECh. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 50ECh. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 52ECh. R.3 - Write the domain of each function given below in...Ch. R.3 - Prob. 54ECh. R.3 - Prob. 55ECh. R.3 - Prob. 56ECh. R.3 - Prob. 57ECh. R.3 - Prob. 58ECh. R.3 - Prob. 59ECh. R.3 - Prob. 60ECh. R.3 - Hourly earnings. Karen works as a contractor,...Ch. R.3 - Sales tax. Marcus plans to spend at most $200 at...Ch. R.3 - Prob. 63ECh. R.3 - Prob. 64ECh. R.3 - Prob. 65ECh. R.3 - Prob. 67ECh. R.3 - Prob. 68ECh. R.3 - Prob. 69ECh. R.3 - Prob. 70ECh. R.3 - Prob. 71ECh. R.3 - Write an equation for a function whose domain is...Ch. R.3 - Prob. 73ECh. R.3 - Prob. 74ECh. R.3 - Prob. 75ECh. R.3 - Prob. 76ECh. R.4 - Graph. List the slope and y-intercept. 1. y=2xCh. R.4 - Prob. 2ECh. R.4 - Prob. 3ECh. R.4 - Prob. 4ECh. R.4 - Prob. 5ECh. R.4 - Graph. List the slope and y-intercept. 6. y=2x5Ch. R.4 - Graph. List the slope and y-intercept. 7....Ch. R.4 - Prob. 8ECh. R.4 - Prob. 9ECh. R.4 - Prob. 10ECh. R.4 - Find the slope and y-intercept. y4x=1Ch. R.4 - Find the slope and y-intercept. y3x=6Ch. R.4 - Find the slope and y-intercept. 2x+y3=0Ch. R.4 - Find the slope and y-intercept.
22.
Ch. R.4 - Find the slope and y-intercept. 3x3y+6=0Ch. R.4 - Find the slope and y-intercept.
24.
Ch. R.4 - Find the slope and y-intercept. x=3y+7Ch. R.4 - Find the slope and y-intercept. x=4y+3Ch. R.4 - For Exercises 19-28, use the given point and slope...Ch. R.4 - Prob. 20ECh. R.4 - For Exercises 19-28, use the given point and slope...Ch. R.4 - Prob. 22ECh. R.4 - For Exercises 19-28, use the given point and slope...Ch. R.4 - For Exercises 19-28, use the given point and slope...Ch. R.4 - For Exercises 19-28, use the given point and slope...Ch. R.4 - Prob. 26ECh. R.4 - Prob. 27ECh. R.4 - Prob. 28ECh. R.4 - For Exercises 29-50, find (a) the slope (if it is...Ch. R.4 - Prob. 30ECh. R.4 - Prob. 31ECh. R.4 - Prob. 32ECh. R.4 - For Exercises 29-50, find (a) the slope (if it is...Ch. R.4 - Prob. 34ECh. R.4 - Prob. 35ECh. R.4 - Prob. 36ECh. R.4 - Prob. 37ECh. R.4 - Prob. 38ECh. R.4 - Prob. 39ECh. R.4 - Prob. 40ECh. R.4 - For Exercises 29-50, find (a) the slope (if it is...Ch. R.4 - For Exercises 29-50, find (a) the slope (if it is...Ch. R.4 - For Exercises 29-50, find (a) the slope (if it is...Ch. R.4 - Prob. 44ECh. R.4 - Prob. 45ECh. R.4 - Prob. 46ECh. R.4 - For Exercises 29-50, find (a) the slope (if it is...Ch. R.4 - Prob. 48ECh. R.4 - Prob. 49ECh. R.4 - Prob. 50ECh. R.4 - 61. Find the slope (or grade) of the treadmill.
Ch. R.4 - Find the slope of the skateboard ramp.Ch. R.4 - Find the slope (or head) of the river. Express the...Ch. R.4 - Prob. 54ECh. R.4 - Prob. 55ECh. R.4 - Prob. 56ECh. R.4 - Highway tolls. It has been suggested that since...Ch. R.4 - Inkjet cartridges. A registrar's office finds that...Ch. R.4 - Prob. 59ECh. R.4 - Profit-and-loss analysis. Red Tide is planning a...Ch. R.4 - Profit-and-loss analysis. Raven Entertainment...Ch. R.4 - Straight-line depreciation. Quick Copy buys an...Ch. R.4 - Prob. 64ECh. R.4 - Prob. 65ECh. R.4 - 72. Straight-line depreciation. Tyline Electric...Ch. R.4 - Stair requirements. A North Carolina state law...Ch. R.4 - Prob. 68ECh. R.4 - Health insurance premiums. Find the average rate...Ch. R.4 - Prob. 70ECh. R.4 - Prob. 71ECh. R.4 - Prob. 72ECh. R.4 - Energy conservation. The R-factor of home...Ch. R.4 - Nerve impulse speed. Impulses in nerve fibers...Ch. R.4 - Muscle weight. The weight M of a persons muscles...Ch. R.4 - 81. Brain weight. The weight B of a person's brain...Ch. R.4 - Prob. 77ECh. R.4 - 83. Reaction time. While driving a car, you see a...Ch. R.4 - Estimating heights. An anthropologist can use...Ch. R.4 - Prob. 80ECh. R.4 - Prob. 82ECh. R.4 - Prob. 83ECh. R.4 - 89. Suppose, and all lie on the same line. Find...Ch. R.4 - Describe one situation in which you would use the...Ch. R.4 - Business: daily sales. Match each sentence below...Ch. R.4 - Business: depreciation. A large crane is being...Ch. R.4 - Graph some of the total-revenue, total-cost, and...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Prob. 2ECh. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Prob. 9ECh. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Prob. 14ECh. R.5 - Graph each pair of equations on one set of axes,...Ch. R.5 - Prob. 16ECh. R.5 - For each of the following quadratic functions, (a)...Ch. R.5 - Prob. 18ECh. R.5 - Prob. 19ECh. R.5 - For each of the following quadratic functions, (a)...Ch. R.5 - For each of the following quadratic functions, (a)...Ch. R.5 - For each of the following quadratic functions, (a)...Ch. R.5 - For each of the following quadratic functions, (a)...Ch. R.5 - Prob. 24ECh. R.5 - Prob. 25ECh. R.5 - Prob. 26ECh. R.5 - Graph, and state the domain using interval...Ch. R.5 - Prob. 28ECh. R.5 - Graph, and state the domain using interval...Ch. R.5 - Graph, and state the domain using interval...Ch. R.5 - Graph, and state the domain using interval...Ch. R.5 - Graph, and state the domain using interval...Ch. R.5 - Graph, and state the domain using interval...Ch. R.5 - Prob. 34ECh. R.5 - Solve. x22x=2Ch. R.5 - Solve. x22x+1=5Ch. R.5 - Solve.
47.
Ch. R.5 - Solve. x2+4x=3Ch. R.5 - Solve. 4x2=4x+1Ch. R.5 - Solve.
50.
Ch. R.5 - Solve. 3y2+8y+2=0Ch. R.5 - Solve. 2p25p=1Ch. R.5 - Solve. x+7+9x=0 (Hint: Multiply both sides by x).Ch. R.5 - Solve. 11w=1w2Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Prob. 46ECh. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Prob. 56ECh. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Prob. 62ECh. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Rewrite each of the following as an equivalent...Ch. R.5 - Simplify.
75.
Ch. R.5 - Simplify.
76.
Ch. R.5 - Simplify.
77.
Ch. R.5 - Simplify. 82/3Ch. R.5 - Determine the domain of each function. f(x)=x225x5Ch. R.5 - Determine the domain of each function. f(x)=x24x+2Ch. R.5 - Determine the domain of each function....Ch. R.5 - Determine the domain of each function....Ch. R.5 - Determine the domain of each function. f(x)=5x+4Ch. R.5 - Determine the domain of each function. f(x)=2x6Ch. R.5 - Determine the domain of each function.
85.
Ch. R.5 - Determine the domain of each function.
86.
Ch. R.5 - Prob. 77ECh. R.5 - Prob. 78ECh. R.5 - Prob. 79ECh. R.5 - Find the equilibrium point for each pair of demand...Ch. R.5 - Find the equilibrium point for each pair of demand...Ch. R.5 - Prob. 82ECh. R.5 - Prob. 83ECh. R.5 - Find the equilibrium point for each pair of demand...Ch. R.5 - 95. Price of admission. The number of tickets sold...Ch. R.5 - Demand. The quantity sold x of a high-definition...Ch. R.5 - 97. Radar Range. The function given by
can be...Ch. R.5 - Find the equilibrium point for each pair of demand...Ch. R.5 - 99. Life Science: pollution control. Pollution...Ch. R.5 - Surface area and mass. The surface area of a...Ch. R.5 - Prob. 91ECh. R.5 - At most, how many y-intercepts can a function...Ch. R.5 - What is the difference between a rational function...Ch. R.5 - Prob. 94ECh. R.5 - Prob. 95ECh. R.5 - Prob. 96ECh. R.5 - Prob. 97ECh. R.5 - Prob. 98ECh. R.5 - Prob. 99ECh. R.5 - Prob. 100ECh. R.5 - Prob. 101ECh. R.5 - Prob. 102ECh. R.5 - Prob. 103ECh. R.5 - Prob. 104ECh. R.5 - Prob. 105ECh. R.5 - Prob. 106ECh. R.6 - For Exercises 1-10, (a) complete an input-output...Ch. R.6 - Prob. 2ECh. R.6 - Prob. 3ECh. R.6 - For Exercises 1-10, (a) complete an input-output...Ch. R.6 - Prob. 5ECh. R.6 - For Exercises 1-10, (a) complete an input-output...Ch. R.6 - Prob. 7ECh. R.6 - Prob. 8ECh. R.6 - Prob. 9ECh. R.6 - Prob. 10ECh. R.6 - Write an equivalent logarithmic equation. 11....Ch. R.6 - Write an equivalent logarithmic equation. 12....Ch. R.6 - Prob. 13ECh. R.6 - Write an equivalent logarithmic equation. 14....Ch. R.6 - Prob. 15ECh. R.6 - Write an equivalent logarithmic equation. 16. 36=6Ch. R.6 - Prob. 17ECh. R.6 - Write an equivalent logarithmic equation. 18....Ch. R.6 - Prob. 19ECh. R.6 - Write an equivalent logarithmic equation. 20. rv=zCh. R.6 - Prob. 21ECh. R.6 - Prob. 22ECh. R.6 - Prob. 23ECh. R.6 - Prob. 24ECh. R.6 - Write an equivalent exponential equation. 25....Ch. R.6 - Write an equivalent exponential equation. 26....Ch. R.6 - Prob. 27ECh. R.6 - Write an equivalent exponential equation. 28....Ch. R.6 - Prob. 29ECh. R.6 - Prob. 30ECh. R.6 - Solve for x without using a calculator. 31....Ch. R.6 - Solve for x without using a calculator. 32....Ch. R.6 - Prob. 33ECh. R.6 - Solve for x without using a calculator. 34....Ch. R.6 - Solve for x without using a calculator. 35....Ch. R.6 - Prob. 36ECh. R.6 - Solve for x without using a calculator. 37....Ch. R.6 - Prob. 38ECh. R.6 - Prob. 39ECh. R.6 - Solve for x without using a calculator. 40....Ch. R.6 - Use the change-of-base formula to find each...Ch. R.6 - Use the change-of-base formula to find each...Ch. R.6 - Prob. 43ECh. R.6 - Prob. 44ECh. R.6 - Prob. 45ECh. R.6 - Use the change-of-base formula to find each...Ch. R.6 - Prob. 47ECh. R.6 - Prob. 48ECh. R.6 - Use the change-of-base formula to find each...Ch. R.6 - Use the change-of-base formula to find each...Ch. R.6 - Prob. 51ECh. R.6 - Solve each equation for x. Give the answers to...Ch. R.6 - Prob. 53ECh. R.6 - Prob. 54ECh. R.6 - Prob. 55ECh. R.6 - Prob. 56ECh. R.6 - Prob. 57ECh. R.6 - Prob. 58ECh. R.6 - Solve each equation for x. Give the answers to...Ch. R.6 - Solve each equation for x. Give the answers to...Ch. R.6 - Given loga2=0.483 and loga3=0.766, use the...Ch. R.6 - Prob. 62ECh. R.6 - Prob. 63ECh. R.6 - Given loga2=0.483 and loga3=0.766, use the...Ch. R.6 - Given loga2=0.483 and loga3=0.766, use the...Ch. R.6 - Given loga2=0.483 and loga3=0.766, use the...Ch. R.6 - Prob. 67ECh. R.6 - Given loga2=0.483 and loga3=0.766, use the...Ch. R.6 - Prob. 69ECh. R.6 - Given loga2=0.483 and loga3=0.766, use the...Ch. R.6 - Sketch the graph of each logarithmic function, and...Ch. R.6 - Sketch the graph of each logarithmic function, and...Ch. R.6 - Prob. 73ECh. R.6 - Prob. 74ECh. R.6 - Prob. 75ECh. R.6 - Sketch the graph of each logarithmic function, and...Ch. R.6 - Casa Grande Technical School had a total...Ch. R.6 - Parker Valley had a population of 12,500 in 2015,...Ch. R.6 - An element undergoes natural radioactive decay....Ch. R.6 - Prob. 80ECh. R.6 - The online program at Accent University had an...Ch. R.6 - The startup GorePoint Inc. had 15 employees...Ch. R.6 - Prob. 83ECh. R.6 - Jenny deposits $5000 into a savings account that...Ch. R.6 - A stock originally worth $50 per share is losing 1...Ch. R.6 - A property originally worth $12,000 is losing 3 of...Ch. R.6 - Prob. 87ECh. R.6 - Prob. 88ECh. R.6 - Prob. 89ECh. R.6 - Prob. 90ECh. R.6 - Prob. 91ECh. R.6 - Prob. 92ECh. R.6 - Prob. 93ECh. R.7 - For the scatter plots and graphs in Exercises 1 9,...Ch. R.7 - For the scatter plots and graphs in Exercises 1 9,...Ch. R.7 - For the scatter plots and graphs in Exercises 1 9,...Ch. R.7 - Prob. 4ECh. R.7 - Prob. 5ECh. R.7 - Prob. 6ECh. R.7 - Prob. 7ECh. R.7 - Prob. 8ECh. R.7 - Prob. 9ECh. R.7 - Average salary in NBA. Use the data from the bar...Ch. R.7 - Prob. 11ECh. R.7 - Absorption of an asthma medication. Use the data...Ch. R.7 - Median household income. Use the data given in...Ch. R.7 - Braking Distance. y=0.144x24.63x+60 Find a...Ch. R.7 - High blood pressure in women. a) Use the first and...Ch. R.7 - Prob. 16ECh. R.7 - Prob. 17ECh. R.7 - Prob. 18ECh. R.7 - Prob. 19ECh. R.7 - In Exercises 17-20, round the numbers in each...Ch. R.7 - 21. Under what conditions might it make better...Ch. R.7 - Prob. 23ECh. R.7 - Prob. 27ECh. R - These review exercises are for test preparation....Ch. R - These review exercises are for test preparation....Ch. R - These review exercises are for test preparation....Ch. R - Prob. 4RECh. R - Prob. 5RECh. R - Prob. 6RECh. R - Prob. 7RECh. R - Prob. 8RECh. R - In Exercises 8 14, classify each statement as...Ch. R - In Exercises 8 14, classify each statement as...Ch. R - Prob. 11RECh. R - In Exercises 8 14, classify each statement as...Ch. R - In Exercises 8 14, classify each statement as...Ch. R - Prob. 14RECh. R - In Exercises 8 – 14, classify each statement as...Ch. R - 15. Hearing-impaired Americans. The following...Ch. R - Finance: compound interest. Sam borrows $4000 at...Ch. R - Business: compound interest. Lucinda invests...Ch. R - Is the following correspondence a function? Why or...Ch. R - A function is given by f(x)=x2+x. Find each of the...Ch. R - Graph. [R.5] f(x)=(x2)2Ch. R - Graph. [R.5] 22. y=x1Ch. R - Graph. [R.5] 23. f(x)=3xx+4Ch. R - Graph. [R.5] g(x)=x+1Ch. R - Use the vertical-line test to determine whether...Ch. R - Use the vertical-line test to determine whether...Ch. R - Use the vertical-line test to determine whether...Ch. R - Use the vertical-line test to determine whether...Ch. R - For the graph of function f shown to the right...Ch. R - 29. Consider the function given by
a. Find ...Ch. R - Use the vertical-line test to determine whether...Ch. R - Write interval notation for each of the following....Ch. R - For the function graphed below, determine (a)...Ch. R - Use the vertical-line test to determine whether...Ch. R - 34. What are the slope and the y-intercept of?
Ch. R - 35. Find an equation of the line with slope,...Ch. R - Find the slope of the line containing the points...Ch. R - Find the average rate of change.
37.
Ch. R - Find the average rate of change. [R.4]Ch. R - Business: shipping charges. The amount A that...Ch. R - 40. Business: profit-and-loss analysis. The band...Ch. R - Prob. 42RECh. R - Graph each of the following. If the graph is a...Ch. R - Solve each of the following. [R.5] a. 5+x2=4x+2 b....Ch. R - Prob. 45RECh. R - 45. Rewrite each of the following as an equivalent...Ch. R - Determine the domain of the function given by...Ch. R - Prob. 48RECh. R - The population of Arvon Hill is given by...Ch. R - Prob. 50RECh. R - Given logb2=0.314 and logb3=0.497: [R.6] a) Find...Ch. R - Prob. 52RECh. R - Prob. 53RECh. R - Prob. 54RECh. R - Prob. 55RECh. R - Prob. 56RECh. R - 52. Economics: demand. The demand function for...Ch. R - Prob. 58RECh. R - Prob. 59RECh. R - Prob. 60RECh. R - Prob. 61RECh. R - Prob. 62RECh. R - Prob. 63RECh. R - Prob. 64RECh. R - Business: compound interest. Cecilia invests funds...Ch. R - Prob. 2TCh. R - Find the slope and they-intercept of the graph of...Ch. R - 4. Find an equation of the line with slope,...Ch. R - Find the slope of the line containing the points...Ch. R - Find the average rate of change.Ch. R - Find the average rate of change.
7.
Ch. R - Life Science: body fluids. The weight F of fluids...Ch. R - 9. Business: profit-and-loss analysis. A printing...Ch. R - Prob. 10TCh. R - Use the vertical-line test to determine whether...Ch. R - Use the vertical-line test to determine whether...Ch. R - 13. For the following graph of a quadratic...Ch. R - Graph: f(x)=8/x.Ch. R - Prob. 15TCh. R - Prob. 16TCh. R - Prob. 17TCh. R - Prob. 18TCh. R - 20. Write interval notation for the following...Ch. R - Prob. 20TCh. R - Prob. 21TCh. R - Graph: f(x)={x2+2,forx0,x22,forx0.Ch. R - Graph and identify the y-intercept: f(x)=12(3)x.Ch. R - Prob. 24TCh. R - Nutrition. As people age their daily caloric needs...Ch. R - 24. Simplify: .
Ch. R - 25. Find the domain and the zeros of the function...Ch. R - Prob. 28TCh. R - 27. A function's average rate of change over the...Ch. R - Graph f and find its zeros, domain, and range:...Ch. R - Prob. 31T
Additional Math Textbook Solutions
Find more solutions based on key concepts
For a population containing N=902 individual, what code number would you assign for a. the first person on the ...
Basic Business Statistics, Student Value Edition
Fill in each blank so that the resulting statement is true.
1. A combination of numbers, variables, and opera...
College Algebra (7th Edition)
1. combination of numbers, variables, and operation symbols is called an algebraic______.
Algebra and Trigonometry (6th Edition)
Calculate the surface area of pillar that needs more painting.
Pre-Algebra Student Edition
A total of 28 percent of American males smoke cigarettes. 7 percent smoke cigars, and 5 percent smoke both ciga...
A First Course in Probability (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Find the exact area inside r=2sin(2\theta ) and outside r=\sqrt(3)arrow_forwardA 20 foot ladder rests on level ground; its head (top) is against a vertical wall. The bottom of the ladder begins by being 12 feet from the wall but begins moving away at the rate of 0.1 feet per second. At what rate is the top of the ladder slipping down the wall? You may use a calculator.arrow_forwardExplain the focus and reasons for establishment of 12.4.1(root test) and 12.4.2(ratio test)arrow_forward
- Use 12.4.2 to determine whether the infinite series on the right side of equation 12.6.5, 12.6.6 and 12.6.7 converges for every real number x.arrow_forwarduse Cauchy Mean-Value Theorem to derive Corollary 12.6.2, and then derive 12.6.3arrow_forwardExplain the focus and reasons for establishment of 12.5.4arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Matrix Factorization - Numberphile; Author: Numberphile;https://www.youtube.com/watch?v=wTUSz-HSaBg;License: Standard YouTube License, CC-BY