Chapter 9.6, Problem 14WE

To determine

To calculate: To identify the conic and find its center and foci and to graph the conic

Answer to Problem 14WE

Conic is an ellipse, center is $\left(-1,1\right)$ and foci are $\left(-1+2\sqrt{2},1\right)$ and $\left(-1-2\sqrt{2},1\right)$

Explanation of Solution

Given information: Equation of conic is $x^2+9y^2+2x-18y+1=0$

Formula Used:

Standard form of the equation of ellipse with center $\left(h,k\right)$ and major axis parallel to x-axis is:

  $\frac{{\left(x-h\right)}^2}{a^2}+\frac{{\left(y-k\right)}^2}{b^2}=1$

Where, $a=$ x-intercept, $b=$ y-intercept, $c^2=a^2-b^2$

When, $a>b$ , foci lies on x-axis and coordinates of foci are $\left(h\pm c,k\right)$

When $b>a$ , foci lies on y-axis and coordinates of foci are $\left(h,k\pm c\right)$

Calculation:

Equation of ellipse is given as follows:

  $x^2+9y^2+2x-18y+1=0$

Rewriting the equation:

  $\begin{array}{l}\left(x^2+2x+1\right)+\left(9y^2-18y+9\right)+-1-9+1=0\\ \left(x^2+2x+1\right)+9\left(y^2-2y+1\right)=9\\ {\left(x+1\right)}^2+9{\left(y-1\right)}^2=9\\ \frac{{\left(x+1\right)}^2}{9}+\frac{{\left(y-1\right)}^2}{1}=1\\ \frac{{\left(x-\left(-1\right)\right)}^2}{3^2}+\frac{{\left(y-1\right)}^2}{1^2}=1\end{array}$

Thus, conic is an ellipse

Comparing the equation with standard form of the equation of ellipse $\frac{{\left(x-h\right)}^2}{a^2}+\frac{{\left(y-k\right)}^2}{b^2}=1$ :

  $\begin{array}{l}a=3\\ b=1\\ \left(h,k\right)=\left(-1,1\right)\end{array}$

Center is $\left(-1,1\right)$

Since $a>b$ , thus foci lies on x-axis.

Also, foci is calculated as follows:

  $c^2=a^2-b^2$

Substituting the values:

  $\begin{array}{l}{c}^2=3^2-1^2\\ c^2=9-1\\ c^2=8\\ c=\pm 2\sqrt{2}\end{array}$

Thus, foci are $\left(-1+2\sqrt{2},1\right)$ and $\left(-1-2\sqrt{2},1\right)$

Plotting the graph of ellipse:

  

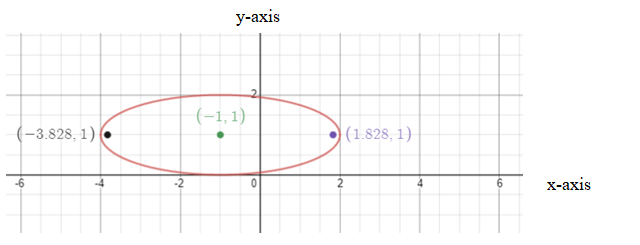
Conclusion:

Hence, conic is an ellipse, center is $\left(-1,1\right)$ and foci are $\left(-1+2\sqrt{2},1\right)$ and $\left(-1-2\sqrt{2},1\right)$