
Find the moment and product of inertia of the area with respect to x and y axes about through
Answer to Problem 9.192RP
The moment of inertia of the area with respect to x about through
The moment of inertia of the area with respect to y about through
The product of inertia of the area with respect to x and y axes about through
Explanation of Solution
Sketch the cross section as shown in Figure 1.

Refer to Figure 9.13.
The moment of inertia
The moment of inertia
Refer to Problem 9.191.
Sketch the cross section as shown in Figure 2.
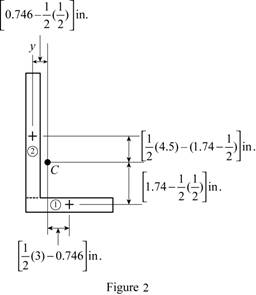
Express the product of inertia as shown below:
Here,
Applying parallel axis theorem,
When the x and y axis is symmetry.
Refer to Figure 1.
Find the area of semicircle section 1 as shown below:
Here,
Substitute
Find the area of rectangle section 2 as shown below:
Here,
Substitute
Find the centroid for section 1 about x axis
Find the centroid for section 1 about x axis
Find the centroid for section 1 about y axis
Find the centroid for section 2 about x axis
Find the product of inertia of the area with respect to x and y axes by using parallel axis theorem as shown below:
Substitute
The Mohr circle is defined by the diameter XY, where
Find the average moment of inertia
Here,
Substitute
Find the radius (R) using the relation as shown below:
Here, R is radius and
Substitute
Sketch the Mohr circle as shown in Figure 3.
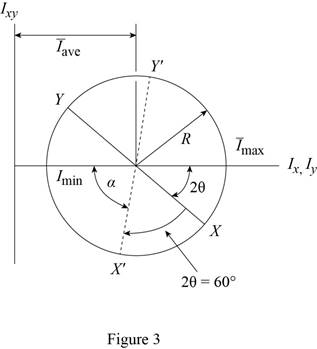
Refer to Figure 2.
Substitute
Find the angle
Find the moment of inertia of the area with respect to x about through
Here,
Substitute
Thus, the moment of inertia of the area with respect to x about through
Find the moment of inertia of the area with respect to y about through
Substitute
Thus, the moment of inertia of the area with respect to y about through
Find the product of inertia of the area with respect to y about through
Substitute
Thus, the product of inertia of the area with respect to x and y axes about through
(b)
Find the orientation of the principal axes through the centroid and corresponding values.
(b)
Answer to Problem 9.192RP
The orientation of the principal axes at the origin is
The maximum moment of inertia is
The minimum moment of inertia is
Explanation of Solution
Calculation:
Find the orientation of the principal axes through at origin as shown below.
Refer part a.
Thus, the orientation of the principal axes at the origin is
Sketch the orientation axis as shown in Figure 4.
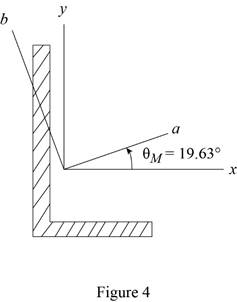
Find the maximum moment
Substitute
Thus, the maximum moment of inertia is
Find the minimum moment
Substitute
Thus, the minimum moment of inertia is
Want to see more full solutions like this?
Chapter 9 Solutions
Vector Mechanics for Engineers: Statics, 11th Edition
- show workingarrow_forwardCFD help Figure 3: Advection equation, solution for three different timesteps. Q1) Provide an explanation what conditions and numerical setup could explain the curves. Identify which of the three curves is the first, second and third timestep.arrow_forwardanswer pleasearrow_forward
- Figure 3 shows the numerical solution of the advection equation for a scalar u along x at three consecutive timesteps. 1.0 0.8- 0.6 0.4- 0.2 0.0 00 -0.2 -0.4 -0.6- 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 Figure 3: Advection equation, solution for three different timesteps.arrow_forwardQuestion 2 Figure 3 shows the numerical solution of the advection equation for a scalar u along x at three consecutive timesteps. 1.0 0.8- 0.6- 0.4- 0.2- 0.0- -0.2- -0.4- -0.6 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 Figure 3: Advection equation, solution for three different timesteps. a) Provide an explanation what conditions and numerical setup could explain the curves. Identify which of the three curves is the first, second and third timestep. b) Consider explicit schemes with central and upwind discretisations. Explain how each of these candidate discretisations could produce the behaviour shown in Figure 3. c) Determine the CFL number that was used in the simulation for each of the candidate schemes for all possible updates. Assume that the timestep and mesh-width used are constant. Read the data to two digits of accuracy from Figure 4 shown at the end of the question, which is an enlarged version of Figure 3. Demonstrate your method and input data for one calculation, but then use a…arrow_forwardanswer pleasearrow_forward
- Provide an explanation what conditions and numerical setup could explain the curves. Identify which of the three curves is the first. second and third timestep.arrow_forwardWhat are the accompanving boundary conditions for this bar?arrow_forward1.1 Consider the fireclay brick wall of Example 1.1 that is operating under different thermal conditions. The tem- perature distribution, at an instant in time, is T(x) = a+ bx where a 1400 K and b = -1000 K/m. Determine the heat fluxes, q", and heat rates, q, at x = 0 and x = L. Do steady-state conditions exist?arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





