
Concept explainers
The expression for stream function.
The plot some streamlines of the flow.
Answer to Problem 63EP
The expression for the stream function is ax2y−bxy22+C.
The following figure represents the streamlines of the flow.
Explanation of Solution
Given information:
The incompressible flow filed for which the velocity u component is u=ax2−bxy, where a=0.45 (ft⋅s)−1, b=0.75 (ft⋅s)−1 and the velocity along the x axis is 0. The stream function along the x axis is 0. The range of x is varies from 0 to 3 and the range of y is varies from 0 to 4.
Write the expression for the velocity along x direction.
v=−∂ψ∂x ....... (I)
Here, the stream function along x direction is ∂ψ, the change in distance along x direction is ∂x and the velocity along x direction is v.
Write the expression for the velocity along x direction.
u=∂ψ∂y ...... (II)
Here, the stream function along y direction is ∂ψ, the change in distance along y direction is ∂y and the velocity along y direction is u.
Write the expression for quadric stream function.
y=ax2±√a2x4−2bxψbx ....... (III)
Here, the stream function is ψ, the distance along x direction is x, the distance along y direction is y and the constants are a and b.
Calculation:
Substitute ax2−bxy for u in Equation (II).
ax2−bxy=∂ψ∂y∂ψ∂y=ax2−bxy∂ψ=(ax2−bxy)⋅∂y ...... (IV)
Integrate Equation (IV) with respect to y.
∂ψ=(ax2−bxy)⋅∂y∫∂ψ=∫(ax2−bxy)⋅∂y+f(x)ψ=ax2y−bxy1+12+f(x)ψ=ax2y−bxy22+f(x) ....... (V)
Here, the constant is f(x).
Substitute ax2y−bxy22+f(x) for ψ and 0 for v in Equation (I).
0=−∂(ax2y−bxy22+f(x))∂x−∂(ax2y−bxy22+f(x))∂x=0 ....... (VI)
Differentiate Equation (V) with respect to x.
−∂(ax2y−bxy22+f(x))∂x=0−2ax2−1y+bx1−1y22−∂f(x)∂x=0−2ax1y+by22−∂f(x)∂x=0 ....... (VII)
Substitute 0 for y in Equation (VII).
−2ax1(0)+b(0)22−∂f(x)∂x=0−∂f(x)∂x=0∂f(x)∂x=0 ....... (VIII)
Substitute 0 for y and C for ψ in Equation (V).
ax2(0)−bx(0)22+f(x)=C0−0+f(x)=Cf(x)=C ....... (IX)
Here, the constant is C.
Substitute C for f(x) in Equation (V).
ψ=ax2y−bxy22+C ....... (X)
Substitute C for f(x) in Equation (X).
ψ=ax2y−bxy22+0ψ=ax2y−bxy22
Substitute 0.45 (ft⋅s)−1 for a and 0.75 (ft⋅s)−1 for b in Equation (III).
y=(0.45 (ft⋅s)−1)x2±√(0.45 (ft⋅s)−1)2x4−2(0.75 (ft⋅s)−1)xψ(0.75 (ft⋅s)−1)xy=0.45 (ft⋅s)−1×x2±√0.2025 (ft⋅s)−1×x4−1.50 (ft⋅s)−1×xψ(0.75 (ft⋅s)−1)x..... (XI)
Substitute 1 for x and 1 for y in Equation (XI).
1=0.45 (ft⋅s)−1×(1)2±√0.2025 (ft⋅s)−1×(1)4−1.50 (ft⋅s)−1×(1)ψ(0.75 (ft⋅s)−1)(1)±√0.2025 (ft⋅s)−1×(1)4−1.50 (ft⋅s)−1×(1)ψ=0.75 (ft⋅s)−1−0.45 (ft⋅s)−10.2025 (ft⋅s)−1×(1)4−1.50 (ft⋅s)−1×(1)ψ=±(0.35 (ft⋅s)−1)2.. (XII)
Solve Equation (XII) by taking positive sign.
0.2025 (ft⋅s)−1×(1)4−1.50 (ft⋅s)−1×(1)ψ=±(0.35 (ft⋅s)−1)2−1.50 (ft⋅s)−1×(1)ψ=−0.08ψ=0.05333
Solve Equation (XII) by taking negative sign.
0.2025 (ft⋅s)−1×(1)4−1.50 (ft⋅s)−1×(1)ψ=−(0.35 (ft⋅s)−1)2−1.50 (ft⋅s)−1×(1)ψ=−0.325ψ=0.216666
The following table shows that the value of stream function with respect to value of x and y.
| x | y | −ψ | +ψ |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 0.216666 | 0.053333 |
| 2 | 2 | 0.4352 | 0.1052 |
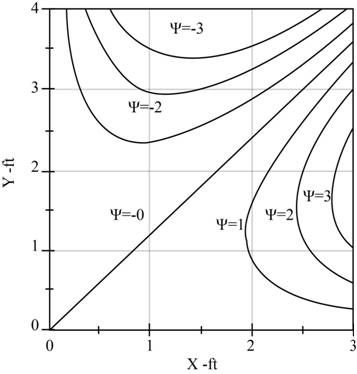
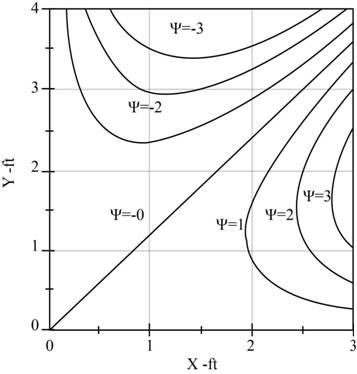
Plot the streamlines on y x plane by using Equation (XII) and the range of x is varies from 0 to 3 and the range of y is varies from 0 to 4.
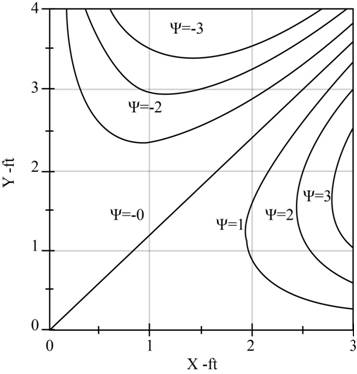
Figure- (1)
The Figure (1) represents the streamlines of the flow.
Conclusion:
The expression for the stream function is ax2y−bxy22+C.
The following figure represents the streamlines of the flow.
Want to see more full solutions like this?
Chapter 9 Solutions
Fluid Mechanics: Fundamentals and Applications
- A rotating shaft is made of 42 mm by 4 mm thick cold-drawn round steel tubing and has a 6 mm diameter hole drilled transversely through it. The shaft is subjected to a pulsating torque fluctuating from 20 to 160 Nm and a completely reversed bending moment of 200 Nm. The steel tubing has a minimum strength of Sut = 410 MPa (60 ksi). The static stress-concentration factor for the hole is 2.4 for bending and 1.9 for torsion. The maximum operating temperature is 400˚C and a reliability of 99.9% is to be assumed. Find the factor of safety for infinite life using the modified Goodman failure criterion.arrow_forwardI need help with a MATLAB code. This code just keeps running and does not give me any plots. I even reduced the tolerance from 1e-9 to 1e-6. Can you help me fix this? Please make sure your solution runs. % Initial Conditions rev = 0:0.001:2; g1 = deg2rad(1); g2 = deg2rad(3); g3 = deg2rad(6); g4 = deg2rad(30); g0 = deg2rad(0); Z0 = 0; w0 = [0; Z0*cos(g0); -Z0*sin(g0)]; Z1 = 5; w1 = [0; Z1*cos(g1); -Z1*sin(g1)]; Z2 = 11; w2 = [0; Z2*cos(g2); -Z2*sin(g2)]; [v3, psi3, eta3] = Nut_angle(Z2, g2, w2); plot(v3, psi3) function dwedt = K_DDE(~, w_en) % Extracting the initial condtions to a variable % Extracting the initial condtions to a variable w = w_en(1:3); e = w_en(4:7); Z = w_en(8); I = 0.060214; J = 0.015707; x = (J/I) - 1; y = Z - 1; s = Z; % Kinematic Differential Equations dedt = zeros(4,1); dedt(1) = pi*(e(3)*(s-w(2)-1) + e(2)*w(3) + e(4)*w(1)); dedt(2) = pi*(e(4)*(w(2)-1-s) + e(3)*w(1) - e(1)*w(3)); dedt(3) = pi*(-e(1)*(s-w(2)-1) - e(2)*w(1) + e(4)*w(3));…arrow_forwardalpha 1 is not zero alpha 1 can equal alpha 2 use velocity triangle to solve for alpha 1 USE MATLAB ONLY provide typed code solve for velocity triangle and dont provide copied answer Turbomachienery . GIven: vx = 185 m/s, flow angle = 60 degrees, (leaving a stator in axial flow) R = 0.5, U = 150 m/s, b2 = -a3, a2 = -b3 Find: velocity triangle , a. magnitude of abs vel leaving rotor (m/s) b. flow absolute angles (a1, a2, a3) 3. flow rel angles (b2, b3) d. specific work done e. use code to draw vel. diagram Use this code for plot % plots Velocity Tri. in Ch4 function plotveltri(al1,al2,al3,b2,b3) S1L = [0 1]; V1x = [0 0]; V1s = [0 1*tand(al3)]; S2L = [2 3]; V2x = [0 0]; V2s = [0 1*tand(al2)]; W2s = [0 1*tand(b2)]; U2x = [3 3]; U2y = [1*tand(b2) 1*tand(al2)]; S3L = [4 5]; V3x = [0 0]; V3r = [0 1*tand(al3)]; W3r = [0 1*tand(b3)]; U3x = [5 5]; U3y = [1*tand(b3) 1*tand(al3)]; plot(S1L,V1x,'k',S1L,V1s,'r',... S2L,V2x,'k',S2L,V2s,'r',S2L,W2s,'b',U2x,U2y,'g',...…arrow_forward
- 3. Find a basis of eigenvectors and diagonalize. 4 0 -19 7 a. b. 1-42 16 12-20 [21-61arrow_forward2. Find the eigenvalues. Find the corresponding eigenvectors. 6 2 -21 [0 -3 1 3 31 a. 2 5 0 b. 3 0 -6 C. 1 1 0 -2 0 7 L6 6 0 1 1 2. (Hint: λ = = 3)arrow_forwardUSE MATLAB ONLY provide typed code solve for velocity triangle and dont provide copied answer Turbomachienery . GIven: vx = 185 m/s, flow angle = 60 degrees, (leaving a stator in axial flow) R = 0.5, U = 150 m/s, b2 = -a3, a2 = -b3 Find: velocity triangle , a. magnitude of abs vel leaving rotor (m/s) b. flow absolute angles (a1, a2, a3) 3. flow rel angles (b2, b3) d. specific work done e. use code to draw vel. diagram Use this code for plot % plots Velocity Tri. in Ch4 function plotveltri(al1,al2,al3,b2,b3) S1L = [0 1]; V1x = [0 0]; V1s = [0 1*tand(al3)]; S2L = [2 3]; V2x = [0 0]; V2s = [0 1*tand(al2)]; W2s = [0 1*tand(b2)]; U2x = [3 3]; U2y = [1*tand(b2) 1*tand(al2)]; S3L = [4 5]; V3x = [0 0]; V3r = [0 1*tand(al3)]; W3r = [0 1*tand(b3)]; U3x = [5 5]; U3y = [1*tand(b3) 1*tand(al3)]; plot(S1L,V1x,'k',S1L,V1s,'r',... S2L,V2x,'k',S2L,V2s,'r',S2L,W2s,'b',U2x,U2y,'g',... S3L,V3x,'k',S3L,V3r,'r',S3L,W3r,'b',U3x,U3y,'g',...... 'LineWidth',2,'MarkerSize',10),...…arrow_forward
- USE MATLAB ONLY provide typed code solve for velocity triangle and dont provide copied answer Turbomachienery . GIven: vx = 185 m/s, flow angle = 60 degrees, R = 0.5, U = 150 m/s, b2 = -a3, a2 = -b3 Find: velocity triangle , a. magnitude of abs vel leaving rotor (m/s) b. flow absolute angles (a1, a2, a3) 3. flow rel angles (b2, b3) d. specific work done e. use code to draw vel. diagram Use this code for plot % plots Velocity Tri. in Ch4 function plotveltri(al1,al2,al3,b2,b3) S1L = [0 1]; V1x = [0 0]; V1s = [0 1*tand(al3)]; S2L = [2 3]; V2x = [0 0]; V2s = [0 1*tand(al2)]; W2s = [0 1*tand(b2)]; U2x = [3 3]; U2y = [1*tand(b2) 1*tand(al2)]; S3L = [4 5]; V3x = [0 0]; V3r = [0 1*tand(al3)]; W3r = [0 1*tand(b3)]; U3x = [5 5]; U3y = [1*tand(b3) 1*tand(al3)]; plot(S1L,V1x,'k',S1L,V1s,'r',... S2L,V2x,'k',S2L,V2s,'r',S2L,W2s,'b',U2x,U2y,'g',... S3L,V3x,'k',S3L,V3r,'r',S3L,W3r,'b',U3x,U3y,'g',...... 'LineWidth',2,'MarkerSize',10),... axis([-1 6 -4 4]), ...…arrow_forwardThe answer should equal to 1157. Please sent me the solution. Thank you!arrow_forwardBONUS: If the volume of the 8cm x 6.5cm x 6cm Block of Aluminum was 312cm3 before machining, find how much material was removed when the fixture below was machined. +2 2.00 cm 6.00 cm 2.50 cm 6.50 cm 1.00 cm 2.50 cm 11.00 cm 8.00 cm 30 CP 9411 FL.4) (m² 1157 Area of triangle = 1/2*B*H Area of circle = лR² Circumference of a circle = 2πR 6.00 cm 6.50 cm 1.50 cm Radius 1.50 cm 1.00 cmarrow_forward
- Consider a 5m by 5m wet concret patio with an average water film thickness of .2mm. Now wind at 50 km/h is blowing over the surface. If the air is at 1 atm, 15oC and 35 percent relative humidity, determine how long it will take for the patio to completely dry.arrow_forward70. Compute the number of cubic centimeters of iron required for the cast-iron plate shown. The plate is 3.50 centimeters thick. Round the answer to the nearest cubic centimeter. 50.0 cm 40.0 cm Radius 150° 115.0 cm- 81.0 cmarrow_forwardLaw of Sines Solve the following problems using the Law of Sin 7. Find side x. All dimensions are in inches. -°-67°-37° 81° x Sin A 8.820 X 67°00' 32°00' a sin A b C sin B sin Carrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





