
Find the reactions and all bar forces for the truss.
Explanation of Solution
Given information:
The Young’s modulus E of the beam is
The area (A) of all the bars is
Identify Zero Force Members:
In a two member forces, if both the members are not parallel and the no external loads or reactions acts at that joint. Then, the force in both the members is zero.
Calculation:
Show the free body diagram of the truss as shown in Figure 1.
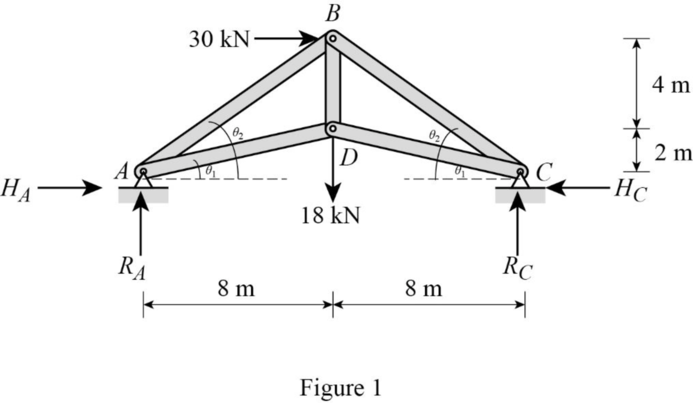
Refer Figure 1.
Find the length of the member AB and BC as follows:
Consider triangle ABD.
By symmetry of truss,
Find the length of the member AD and DC as follows:
Consider triangle ADC.
By symmetry of truss,
Find the angle
Find the angle
Consider the horizontal reaction at C as the redundant.
Remove the redundant at C to get the released structure.
Show the released structure with applied load as shown in Figure 2.

Refer Figure 2.
Find the reactions at A, D, and C as follows:
Apply Equation of Equilibrium,
Find the forces
Refer Figure 2.
Consider Joint C.
Apply Equation of Equilibrium,
Consider joint B.
Apply Equation of Equilibrium,
Consider joint D.
Apply Equation of Equilibrium,
Show the P forces in the members of the truss due to the applied load at C as shown in Table 1.
| Members | |
| AB | |
| BC | |
| AD | |
| DC | |
| DB |
Table 1
Show the released structure loaded with unit horizontal load at C as shown in Figure 2.
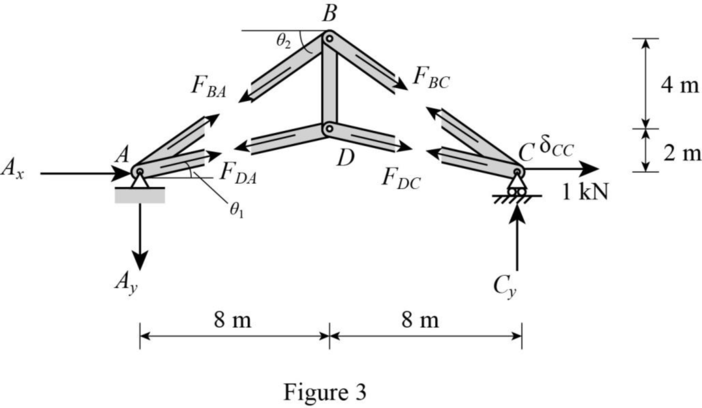
Refer Figure 3.
By symmetry of the truss,
Consider Joint D.
Apply Equation of Equilibrium,
Solve Equation (1) and (2).
By symmetry of the truss,
Consider Joint B.
Apply Equation of Equilibrium,
Show the Q forces in the members of the truss due to the unit load at C as shown in Table 2.
| Members | |
| AB | |
| BC | |
| CD | |
| AC | |
| DB |
Table 2
Find the deflection
| Members | |||||
| AB | 10 | ||||
| BC | 10 | ||||
| AD | 8.246 | ||||
| DC | 8.246 | ||||
| DB | 4 |
Table 3
Refer Table 3.
Find the horizontal reaction at C as follows:
Thus, the horizontal reaction at C is
Find final forces in the truss as shown in Table 4.
| Members | ||||
| AB | -31.89 | 6.80 | ||
| BC | -31.89 | -30.7 | ||
| AD | -31.89 | -7.5 | ||
| DC | -31.89 | -7.5 | ||
| DB | -31.89 | 14.34 |
Table 4
Show the final support reaction as shown in Table 5.
| Support Reactions | ||||
| Members | ||||
| -30 | -1 | -31.89 | 1.89 | |
| -2.25 | 0 | -31.89 | -2.25 | |
| 20.25 | 1 | -31.89 | 20.25 | |
Table 5
Thus, the reactions and all bar forces for the truss is tabulate in table 4 and table 5.
Want to see more full solutions like this?
Chapter 9 Solutions
Fundamentals of Structural Analysis
- Q1: Compute the missing measurement of the lines AB & CD (using trigonometric method), and the coordinates of closed loop traverse ABCD as shown in the figure below. C 20 (due N) N 73° 18' E B S 41° 12' E མམ་བ A (100, 100) D 60 (due W)arrow_forwardPlease solve all points with explanationarrow_forwardPlease solve with drawingarrow_forward
- Please provide a handwritten solution to the questionarrow_forwardName: Q.1 select the lightest W12 shape for column AB that support a service dead and live loads Po-150k and P-200k as shown in Figure. The beams and columns are oriented about the major axis and the columns are braced at top and mid-height using pinned end connections for out of plane buckling. ASTM A992 steel is used. Select the suitable answer below: I U B 8.00 All dimensions in feet 30.00 W18.76 8091 B Parrow_forward2) Determine volume of bioreactor SP 2nd order kinetics. V= ks2 Yieldsarrow_forward
- The question is in Turkish You need to explain the process in detailarrow_forwardQ3. Design by LRFD maximum size side SMAW fillet welds required to develop the loads Po= 7. kips and PL-60kips for an L6x4x1/2, using E70XX electrodes steel. The member is connected on the sides of the 6-in leg and is subject to alternating loads. Draw the layout of welding. Note: 1-5/8 in. 1. All Steel sections are A36 2. The loads effect through the angle center of gravity. L6x4x1/2 Angle C.G. Parrow_forwardDesign the size side SMAW fillet welds required to develop the loads PD= 7. kips and PL=60kips for an L6x4x1/2, using E70XX electrodes steel. The member is to be connected with side welds and a weld at the end of the Q2 angle to a 5/8- inch thickness gusset plate. Balance the fillet welds around the center of gravity of the angle as shown in Figure (2). Use A36 steel. Draw the layout of welding. t=5/8 in. L 6x4x1/2 Angle C.G. P4 Figure -2-arrow_forward
- 1. What is length of a curve if the design speed is 85mph. A grades of a road is 3% and -2% and has stopping sight distance is 820ft. Determine whether S<L or S>Larrow_forward3. A crest vertical curve joins a +3% and -4% grade. Design speed is 75 mph. Length = 2184.0 ft. Station at VPI is 325+ 55.00, elevation at VPI = 260 feet. Find elevations and station for VPC (BVC) and VPT (EVC). 4. On a 0.5-mile highway segment, if the speeds of these 8 vehicles are measured as 55, 45, 40, 50, 60, 65, 70 and 65mph, respectively, what is time mean speed? What is space mean speed. 5. An observer located at point X counted 6 vehicles passing through this point during a period of 45 seconds. What is the hourly flow rate based on the observation? Good Lucky DDA 0 IN INEERI Enginearrow_forward4. On a 0.5-mile highway segment, if the speeds of these 8 vehicles are measured as 55, 45, 40, 50, 60, 65, 70 and 65mph, respectively, what is time mean speed? What is space mean speed.arrow_forward

 Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning





