
Concept explainers
a.
Fill the missing values in the table and to make conclusion about the test.
a.
Answer to Problem 138SE
The completed table is,
| variable | N | St dev | SE Mean | Z | P | |
| x | 14 | 26.541 | 2.032 | 0.401 | 1.3495 | 0.0886 |
Explanation of Solution
Calculation:
The SE Mean from the sample standard deviation is,
Thus, the value of
The value of
Substitute the values,
Thus, the value of
Substituting the value
Software procedure:
Step by step procedure to obtain the P-value using the MINITAB software:
- Choose Calc > Probability Distribution> Normal Distribution.
- Choose Cumulative probability.
- In Input constant, enter 1.3495.
- Click OK.
Output using MINITAB software is given below:

Thus, the P-value is,
Thus, the P-value is 0.0886.
b.
Check whether it is one sided test or two sided test.
b.
Answer to Problem 138SE
The test is one sided.
Explanation of Solution
Justification:
The hypothesis to be tested is
Thus, the test is one sided test.
c.
Find the conclusion about the test if
c.
Answer to Problem 138SE
The null hypothesis is not rejected at 5% level of significance.
Explanation of Solution
Justification:
From the results of part (a), the P-value is 0.0886, which is greater than significance level
d.
Construct a 95% two sided confidence interval for the mean.
d.
Answer to Problem 138SE
The 95% two sided confidence interval for the mean is (25.7553, 27.3268).
Explanation of Solution
Calculation:
The 95% confidence interval for the mean is,
Substitute
Software procedure:
Step by step procedure to obtain
- Choose Graph > Probability Distribution Plot > View Single, and then click OK.
- From Distribution, choose ‘Normal’ distribution.
- Click the Shaded Area tab.
- Choose Probability and both tails for the region of the curve to shade.
- Enter the value as 0.05.
- Click OK.
Output using MINITAB software is given below:
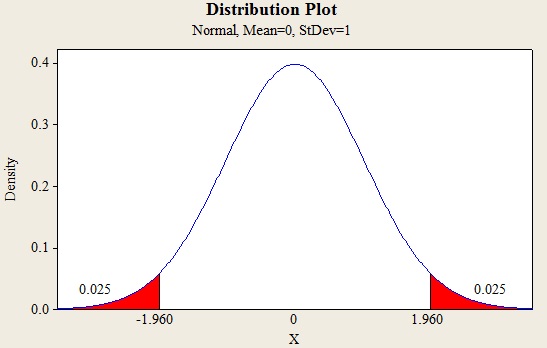
From the MINITAB output, the critical values are,
Substituting the value, the 95% confidence interval for the mean is,
Thus, the 95% confidence interval for the mean is (25.7553, 27.3268).
Want to see more full solutions like this?
Chapter 9 Solutions
Applied Statistics And Probability For Engineers 6e Binder Ready Version + Wileyplus Registration Card
- 19. Let X be a non-negative random variable. Show that lim nE (IX >n)) = 0. E lim (x)-0. = >arrow_forward(c) Utilize Fubini's Theorem to demonstrate that E(X)= = (1- F(x))dx.arrow_forward(c) Describe the positive and negative parts of a random variable. How is the integral defined for a general random variable using these components?arrow_forward
- 26. (a) Provide an example where X, X but E(X,) does not converge to E(X).arrow_forward(b) Demonstrate that if X and Y are independent, then it follows that E(XY) E(X)E(Y);arrow_forward(d) Under what conditions do we say that a random variable X is integrable, specifically when (i) X is a non-negative random variable and (ii) when X is a general random variable?arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





