
A manufacturer produces two models of patio furniture. Model
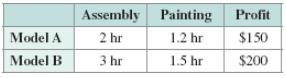
The manufacturer has
a. Determine the number of model
b. What is the maximum profit under these constraints?
c. If the profit on model
Want to see the full answer?
Check out a sample textbook solution
Chapter 8 Solutions
Precalculus
Additional Math Textbook Solutions
Thinking Mathematically (6th Edition)
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
University Calculus: Early Transcendentals (4th Edition)
Calculus: Early Transcendentals (2nd Edition)
Introductory Statistics
Elementary Statistics (13th Edition)
- Redo Exercise 5, assuming that the house blend contains 300 grams of Colombian beans, 50 grams of Kenyan beans, and 150 grams of French roast beans and the gourmet blend contains 100 grams of Colombian beans, 350 grams of Kenyan beans, and 50 grams of French roast beans. This time the merchant has on hand 30 kilograms of Colombian beans, 15 kilograms of Kenyan beans, and 15 kilograms of French roast beans. Suppose one bag of the house blend produces a profit of $0.50, one bag of the special blend produces a profit of $1.50, and one bag of the gourmet blend produces a profit of $2.00. How many bags of each type should the merchant prepare if he wants to use up all of the beans and maximize his profit? What is the maximum profit?arrow_forwardThe manufacturer of a weight training bench spends $15 to build each bench and sells them for $32. The manufacturer also has fixed costs each month of $25,500. (a) Find the cost function C when x benches are manufactured. (b) Find the revenue function R when x benches are sold. (c) Show the break-even point by graphing both the Revenue and Cost functions on the same grid. (d) Find the break-even point. Interpret what the break-even point means.arrow_forwardAt the Pizza Dude restaurant, a 12-in. pizza costs 5.40 to make, and the manager wants to make at least 4.80 from the sale of each pizza. If the pizza will be sold by the slice and each pizza is cut into 6 pieces, what is the minimum charge per slice?arrow_forward
- If during the following year it is predicted that each comedy skit will generate 30 thousand and each musical number 20 thousand, find the maximum income for the year. A television program director must schedule comedy skits and musical numbers for prime-time variety shows. Each comedy skit requires 2 hours of rehearsal time, costs 3000, and brings in 20,000 from the shows sponsors. Each musical number requires 1 hour of rehearsal time, costs 6000, and generates 12,000. If 250 hours are available for rehearsal and 600,000 is budgeted for comedy and music, how many segments of each type should be produced to maximize income? Find the maximum income.arrow_forwardInventories An electronics store manager stocks from 20 to 30 IBM-compatible computers and from 30 to 50 Apple computers. There is room in the store to stock up to 60 computers. The manager receives a commission of 50 on the sale of each IBM-compatible computer and 40 on the sale of each Apple computer. If the manager can sell all of the computers, how many should she stock to maximize her commissions? Find the maximum commission. Inventory IBM Apple Minimum 20 30 Maximum 30 50 Commission 50 40arrow_forwardThe manufacturer of an energy drink spends $1.20 to make each drink and sells them for $2. The manufacturer also has fixed costs each month of $8,000. (a) Find the cost function C when x energy drinks aremanufactured. (b) Find the revenue function R when x drinks are sold. (c) Show the break-even point by graphing both the Revenue and Cost functions on the same grid. (d) Find the break-even point. Interpret what the breakeven point means.arrow_forward
- A manufacturer produces two models of television stands. The table at the left shows the times (in hours) required for assembling, staining, and packaging the two models. The total times available for assembling, staining, and packaging are 3750 hours, 8950 hours, and 2650 hours, respectively. The profits per unit are $30 for model I and $40 for model II. What is the optimal inventory level for each model? What is the optimal profit?arrow_forwardThe manufacturer of a water bottle spends $5 to build each bottle and sells them for $10. The manufacturer also has fixed costs each month of $6500. (a) Find the cost function C when x bottles are manufactured. (b) Find the revenue function R when x bottles are sold. (c) Show the break-even point by graphing both the Revenue and Cost functions on the same grid. (d) Find the break-even point. Interpret what the break-even point means.arrow_forward
 Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning





