Linear Algebra and Its Applications (5th Edition)

5th Edition

ISBN: 9780321982384

Author: David C. Lay, Steven R. Lay, Judi J. McDonald

Publisher: PEARSON

See similar textbooks

Concept explainers

Minimization

In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…

Maxima and Minima

The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.

Derivatives

A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …

Concavity

In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …

Videos

Textbook Question

Chapter 8.6, Problem 1PP

A spline usually refers to a curve that passes through specified points. A B-spline, however, usually does not pass through its control points. A single segment has the parametric form

$x ( t ) = 1 6 [ ( 1 − t ) 3 p 0 + ( 3 t 3 − 6 t 2 + 4 ) p 1 + ( − 3 t 3 + 3 t 2 + 3 t + 1 ) p 2 + t 3 p 3 ]$ (14)

for 0 ≤ t ≤ 1. where p₀, p₁, p₂, and p₃ are the control points. When t varies from 0 to 1, x(t) creates a short curve that lies close to $p 1 p 2 ¯$ . Basic algebra shows that the B-spline formula can also be written as

$x ( t ) = 1 6 [ ( 1 − t ) 3 p 0 + ( 3 t ( 1 − t ) 2 − 3 t + 4 ) p 1 + ( 3 t 2 ( 1 − t ) + 3 t + 1 ) p 2 + t 3 p 3 ]$ (15)

This shows the similarity with the Bézier curve. Except for the 1/6 factor at the front, the p₀ and p₃ terms are the same. The p₁ component has been increased by – 3t + 4 and the p₂ component has been increased by 3t + 1. These components move the curve closer to $p 1 p 2 ¯$ than the Bézier curve. The 1/6 factor is necessary to keep the sum of the coefficients equal to 1. Figure 10 compares a B-spline with a Bézier curve that has the same control points.

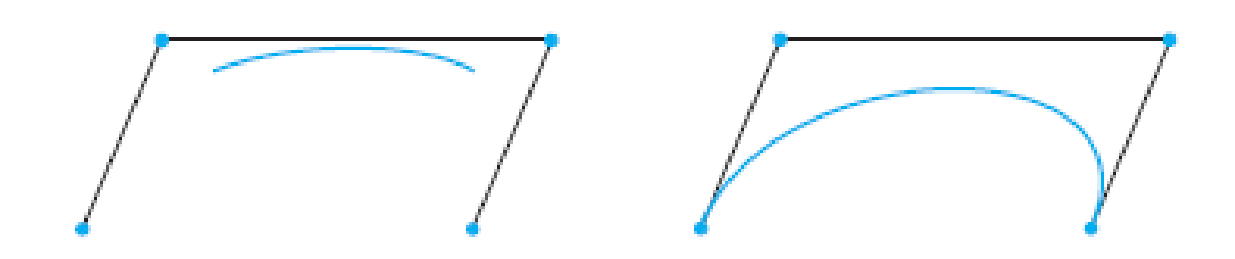
Chapter 8.6, Problem 1PP, A spline usually refers to a curve that passes through specified points. A B-spline, however,

FIGURE 10 A B-spline segment and a Bézier curve.

1. Show that the B-spline does not begin at p₀, but x(0) is in conv {p₀, p₁, p₂}. Assuming that p₀, p₁, and p₂ are affinely independent, find the affine coordinates of x(0) with respect to {p₀, p₁, p₂}.

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 8.5, Problem 22E

Chapter 8.6, Problem 2PP

Students have asked these similar questions

Safari File Edit View History Bookmarks Window Help Ο Ω OV O mA 0 mW ర Fri Apr 4 1 222 tv A F9 F10 DII 4 F6 F7 F8 7 29 8 00 W E R T Y U S D பட 9 O G H J K E F11 + 11 F12 O P } [

So confused. Step by step instructions please

In simplest terms, Sketch the graph of the parabola. Then, determine its equation. opens downward, vertex is (- 4, 7), passes through point (0, - 39)

Chapter 8 Solutions

Linear Algebra and Its Applications (5th Edition)

Ch. 8.1 - Plot the points v1=[10],v2=[12], v3=[31], and...Ch. 8.1 - In Exercises 14, write y as an affine combination...Ch. 8.1 - In Exercises 14, write y as an affine combination...Ch. 8.1 - In Exercises 14, write y as an affine combination...Ch. 8.1 - In Exercises 14, write y as an affine combination...Ch. 8.1 - Prob. 5E Ch. 8.1 - Prob. 6E Ch. 8.1 - Prob. 7E Ch. 8.1 - Prob. 8E Ch. 8.1 - Prob. 9E

Ch. 8.1 - Suppose that the solutions of an equation Ax = b...Ch. 8.1 - Prob. 11E Ch. 8.1 - a. If S = {x}, then aff S is the empty set. b. A...Ch. 8.1 - Prob. 13E Ch. 8.1 - Prob. 14E Ch. 8.1 - Prob. 15E Ch. 8.1 - Prob. 16E Ch. 8.1 - Choose a set S of three points such that aff S is...Ch. 8.1 - Prob. 18E Ch. 8.1 - Prob. 19E Ch. 8.1 - Prob. 20E Ch. 8.1 - Prob. 21E Ch. 8.1 - Prob. 22E Ch. 8.1 - Prob. 23E Ch. 8.1 - Prob. 24E Ch. 8.1 - Prob. 25E Ch. 8.1 - Prob. 26E Ch. 8.2 - Describe a fast way to determine when three points...Ch. 8.2 - Prob. 2PP Ch. 8.2 - Prob. 1E Ch. 8.2 - Prob. 2E Ch. 8.2 - Prob. 3E Ch. 8.2 - Prob. 4E Ch. 8.2 - Prob. 5E Ch. 8.2 - Prob. 6E Ch. 8.2 - Prob. 7E Ch. 8.2 - Prob. 8E Ch. 8.2 - In Exercises 9 and 10, mark each statement True or...Ch. 8.2 - a. If{v1,....,vp} is an affinely dependent set in...Ch. 8.2 - Prob. 11E Ch. 8.2 - Prob. 12E Ch. 8.2 - Prob. 13E Ch. 8.2 - The conditions for affine dependence are stronger...Ch. 8.2 - Prob. 15E Ch. 8.2 - Prob. 16E Ch. 8.2 - Prob. 17E Ch. 8.2 - Let T be a tetrahedron in standard position, with...Ch. 8.2 - Prob. 19E Ch. 8.2 - Prob. 20E Ch. 8.2 - In Exercises 21-24, a, b, and c are noncollinear...Ch. 8.2 - Prob. 22E Ch. 8.2 - Prob. 23E Ch. 8.2 - Prob. 24E Ch. 8.2 - Prob. 25E Ch. 8.2 - Prob. 26E Ch. 8.3 - Prob. 1PP Ch. 8.3 - Let S be the set of points on the curve y = 1/x...Ch. 8.3 - Prob. 1E Ch. 8.3 - Describe the convex hull of the set S of points...Ch. 8.3 - Prob. 3E Ch. 8.3 - Prob. 4E Ch. 8.3 - Prob. 5E Ch. 8.3 - Prob. 6E Ch. 8.3 - Prob. 7E Ch. 8.3 - Prob. 8E Ch. 8.3 - Prob. 9E Ch. 8.3 - Repeat Exercise 9 for the points q1, , q5 whose...Ch. 8.3 - Prob. 11E Ch. 8.3 - In Exercises 11 and 12, mark each statement True...Ch. 8.3 - Prob. 13E Ch. 8.3 - Prob. 14E Ch. 8.3 - Let v1 = [10], v2 = [12], v3 = [42], v4 = [40],...Ch. 8.3 - Prob. 16E Ch. 8.3 - In Exercises 17-20, prove the given statement...Ch. 8.3 - In Exercises 17-20, prove the given statement...Ch. 8.3 - Prob. 19E Ch. 8.3 - Prob. 20E Ch. 8.3 - Prob. 21E Ch. 8.3 - Prob. 22E Ch. 8.3 - Prob. 23E Ch. 8.3 - Prob. 24E Ch. 8.4 - Prob. 1PP Ch. 8.4 - Let L be the line in 2 through the points [14] and...Ch. 8.4 - Prob. 2E Ch. 8.4 - Prob. 3E Ch. 8.4 - In Exercises 3 and 4, determine whether each set...Ch. 8.4 - Prob. 5E Ch. 8.4 - Prob. 6E Ch. 8.4 - Prob. 7E Ch. 8.4 - Prob. 8E Ch. 8.4 - Prob. 9E Ch. 8.4 - In Exercises 7-10, let H be the hyperplane through...Ch. 8.4 - Prob. 11E Ch. 8.4 - Let a1=[215], a2=[313], a3=[160], b1=[051],...Ch. 8.4 - Prob. 13E Ch. 8.4 - Let F1 and F2 be 4-dimensional flats in 6, and...Ch. 8.4 - In Exercises 15-20, write a formula for a linear...Ch. 8.4 - Prob. 16E Ch. 8.4 - Prob. 17E Ch. 8.4 - In Exercises 15-20, write a formula for a linear...Ch. 8.4 - Prob. 19E Ch. 8.4 - Prob. 20E Ch. 8.4 - Prob. 21E Ch. 8.4 - Prob. 22E Ch. 8.4 - Prob. 23E Ch. 8.4 - Prob. 24E Ch. 8.4 - Let p=[41], Find a hyperplane [f : d] that...Ch. 8.4 - Let q=[23] and p=[61]. Find a hyperplane [f : d]...Ch. 8.4 - Prob. 27E Ch. 8.4 - Prob. 28E Ch. 8.4 - Prob. 29E Ch. 8.4 - Prove that the convex hull of a bounded set is...Ch. 8.5 - Find the minimal representation of the polytope P...Ch. 8.5 - Given points p1 = [10], p2 = [23], and p3 = [12]...Ch. 8.5 - Given points p1 = [01], p2 = [21], and p3 = [12]...Ch. 8.5 - Repeat Exercise 1 where m is the minimum value of...Ch. 8.5 - Repeat Exercise 2 where m is the minimum value of...Ch. 8.5 - In Exercises 5-8, find the minimal representation...Ch. 8.5 - In Exercises 5-8, find the minimal representation...Ch. 8.5 - In Exercises 5-8, find the minimal representation...Ch. 8.5 - In Exercises 5-8, find the minimal representation...Ch. 8.5 - Let S = {(x, y) : x2 + (y 1)2 1} {(3, 0)}. Is...Ch. 8.5 - Find an example of a closed convex set S in 2 such...Ch. 8.5 - Find an example of a bounded convex set S in 2...Ch. 8.5 - a. Determine the number of k-faces of the...Ch. 8.5 - a. Determine the number of k-faces of the...Ch. 8.5 - Suppose v1, , vk are linearly independent vectors...Ch. 8.5 - A k-pyramid Pk is the convex hull of a (k ...Ch. 8.5 - Prob. 16E Ch. 8.5 - In Exercises 16 and 17, mark each statement True...Ch. 8.5 - Let v be an element of the convex set S. Prove...Ch. 8.5 - If c and S is a set, define cS = {cx : x S}....Ch. 8.5 - Find an example to show that the convexity of S is...Ch. 8.5 - Prob. 21E Ch. 8.5 - Prob. 22E Ch. 8.6 - A spline usually refers to a curve that passes...Ch. 8.6 - Prob. 2PP Ch. 8.6 - Prob. 1E Ch. 8.6 - Prob. 2E Ch. 8.6 - Prob. 3E Ch. 8.6 - Prob. 4E Ch. 8.6 - Prob. 5E Ch. 8.6 - Prob. 6E Ch. 8.6 - Let x(t) and y(t) be Bzier curves from Exercise 5,...Ch. 8.6 - Prob. 8E Ch. 8.6 - Prob. 9E Ch. 8.6 - Prob. 10E Ch. 8.6 - In Exercises 11 and 12, mark each statement True...Ch. 8.6 - In Exercises 11 and 12, mark each statement True...Ch. 8.6 - Prob. 13E Ch. 8.6 - Prob. 14E Ch. 8.6 - Prob. 15E Ch. 8.6 - Explain why a cubic Bzier curve is completely...Ch. 8.6 - TrueType fonts, created by Apple Computer and...Ch. 8.6 - Prob. 18E

Additional Math Textbook Solutions

Find more solutions based on key concepts

First Derivative Test a. Locale the critical points of f. b. Use the First Derivative Test to locale the local ...

Calculus: Early Transcendentals (2nd Edition)

Check Your Understanding Reading Check Complete each sentence using > or < for □. RC1. 3 dm □ 3 dam

Basic College Mathematics

Find how many SDs above the mean price would be predicted to cost.

Intro Stats, Books a la Carte Edition (5th Edition)

23. A plant nursery sells two sizes of oak trees to landscapers. Large trees cost the nursery $120 from the gro...

College Algebra (Collegiate Math)

The largest polynomial that divides evenly into a list of polynomials is called the _______.

Elementary & Intermediate Algebra

In the following exercises, multiply the monomials. 138. (14d5)(36d2)

Elementary Algebra

Knowledge Booster

$Algebra$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.

Solution Summary: The author explains that the B-spline does not begin at p_0, but it's in the affine coordinates.

Concept explainers

Videos

Want to see the full answer?

Chapter 8 Solutions

Additional Math Textbook Solutions