
Concept explainers
Soccer Angles A soccer goal is 8 yards wide. Suppose a goalie is standing on her line in the center of her goal as a striker from the opposing team moves the ball towards her. The near post angle, , is formed by rays extending from the ball to the near post and the goalie. Similarly, the far post angle, , is formed by rays extending from the ball to the far post and the goalie. See the figure.
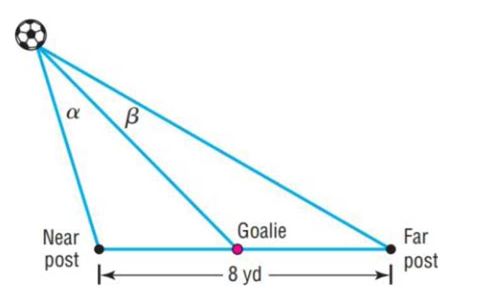
a. Determine the near post angle and the far post angle when the striker is 20 yards from the near post and 24 yards from the far post.
b. How far is the goalie from the ball?
c. To cover the near post, the goalie moves toward the near post in order to make the near post angle and the far post angle equal. How far toward her near post does the goalie need to move?
Want to see the full answer?
Check out a sample textbook solution
Chapter 8 Solutions
Precalculus
- the second is the Problem 1 solution.arrow_forwardc) Sketch the grap 109. Hearing Impairments. The following function approximates the number N, in millions, of hearing-impaired Americans as a function of age x: N(x) = -0.00006x³ + 0.006x2 -0.1x+1.9. a) Find the relative maximum and minimum of this function. b) Find the point of inflection of this function. Sketch the graph of N(x) for 0 ≤ x ≤ 80.arrow_forwardThe purpose of this problem is to solve the following PDE using a numerical simulation. { af (t, x) + (1 − x)= - Ət af 10²ƒ + მე 2 მე2 = 0 f(ln(2), x) = ex (a) The equation above corresponds to a Feynman-Kac formula. Identify the stochastic process (X)20 and the expectation that would correspond to f(t, x) explicitly. (b) Use a numerical simulation of (X+) above to approximate the values of f(0, x) at 20 discrete points for x, uniformly spaced in the interval [0,2]. Submit a graph of your solution. (c) How would you proceed to estimate the function f(0.1, x). (Briefly explain your method, you do not need to do it.) Extra question: You can explicitly determine the function in (b) (either as a conditional expectation or by solving the PDE). Compare the theoretical answer to your solution.arrow_forward
- A sequence is given by the formula an = n/2n^2 +1 . Show the sequence is monotone decreasing for n >1. (Hint: What tool do you know for showing a function is decreasing?)arrow_forwardA sequence is given by the formula an = n 2n2 +1 . Show the sequence is monotone decreasing for n 1. (Hint: What tool do you know for showing a function is decreasing?)arrow_forwardDifferentiate #32, #35arrow_forward
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning





