Understanding Basic Statistics
7th Edition
ISBN: 9781305254060
Author: Charles Henry Brase, Corrinne Pellillo Brase
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 8.2, Problem 19P
19
Critical Thinking: Boxplots and Confidence Intervals The distribution of heights of 18-year-old men in the United States is approximately normal. with
| VARIABLE | N | MEAN | STDEV | SEMEAN | 95.0 | % CI |
| Sample 1 | 20 | 68.050 | 2.901 | 0.649 | 69.407) | |
| Sample a | 20 | 67.956 | 3.137 | 0.702 | (66.490 | 69.426 |
| Sample 3 | 20 | 67.976 | 2.639 | 0.590 | (66.741 , | 69.211) |
| Sample 4 | 20 | 66.908 | 2.440 | 0.546 | (65.766 , | 68.050) |
(a) Examine the figure (parts (a) to (d)). How do the boxplots for the four samples differ? Why should you expect the boxplots to differ ?
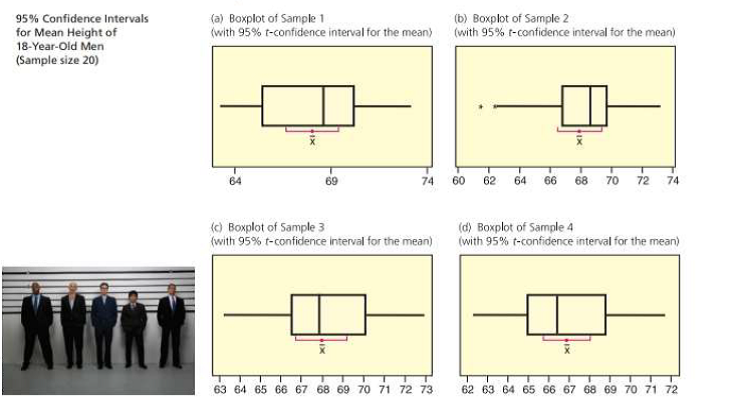
(b) Examine the 95% confidence intervals for the four sample shown in the printout. Do the intervals differ in length? Do the intervals all contain the expected population mean of tot inches? If we draw more samples, do you expect all of the resulting 95% confidence intervals to contain µ = 68 ? Why or why not?
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Throughout, A, B, (An, n≥ 1), and (Bn, n≥ 1) are subsets of 2.
1. Show that
AAB (ANB) U (BA) = (AUB) (AB),
Α' Δ Β = Α Δ Β,
{A₁ U A2} A {B₁ U B2) C (A1 A B₁}U{A2 A B2).
16. Show that, if X and Y are independent random variables, such that E|X|< ∞,
and B is an arbitrary Borel set, then
EXI{Y B} = EX P(YE B).
Proposition 1.1 Suppose that X1, X2,... are random variables. The following
quantities are random variables:
(a) max{X1, X2) and min(X1, X2);
(b) sup, Xn and inf, Xn;
(c) lim sup∞ X
and lim inf∞ Xn-
(d) If Xn(w) converges for (almost) every w as n→ ∞, then lim-
random variable.
→ Xn is a
Chapter 8 Solutions
Understanding Basic Statistics
Ch. 8.1 - In Problems 1-8, answer true or false. Explain...Ch. 8.1 - In Problems 1-8, answer true or false. Explain...Ch. 8.1 - In Problems 1-8, answer true or false. Explain...Ch. 8.1 - In Problems 1-8, answer true or false. Explain...Ch. 8.1 - In Problems 1-8, answer true or false. Explain...Ch. 8.1 - In Problems 1-8, answer true or false. Explain...Ch. 8.1 - In Problems 1-8, answer true or false. Explain...Ch. 8.1 - In Problems 1-8, answer true or false. Explain...Ch. 8.1 - Critical Thinking Sam computed a 95% confidence...Ch. 8.1 - Critical Thinking Sam computed a 90% confidence...
Ch. 8.1 - Basic Computation: Confidence Interval Suppose x...Ch. 8.1 - Basic Computation:Confidence Interval Suppose x...Ch. 8.1 - Basic Computation: Sample Size Suppose x has a...Ch. 8.1 - Basic Computation: Sample Size Suppose x has a...Ch. 8.1 - Zoology: Hummingbirds Allen's hummingbird...Ch. 8.1 - Diagnostic Tests: Uric Acid Overproduction of uric...Ch. 8.1 - Diagnostic Tests: Plasma Volume Total plasma...Ch. 8.1 - Agriculture: Watermelon What price do farmers get...Ch. 8.1 - FBI Report: Larceny Thirty small communities in...Ch. 8.1 - Confidence Intervals: Values of A random sample...Ch. 8.1 - Confidence Intervals: Sample Size A random sample...Ch. 8.1 - Ecology: Sand Dunes At wind speeds above 1000...Ch. 8.1 - Profits: Banks Jobs and productivity! How do banks...Ch. 8.1 - Prob. 24PCh. 8.1 - Ballooning: Air Temperature How hot is the air in...Ch. 8.2 - Use Table 4 of the Appendix to find tc for a 0.95...Ch. 8.2 - Use Table 4 of the Appendix to find tc for a 0.99...Ch. 8.2 - Use Table 4 of the Appendix to find tc for a 0.90...Ch. 8.2 - Use Table 4 of the Appendix to find tc for a 0.95...Ch. 8.2 - Statistical Literacy Students t distributions are...Ch. 8.2 - Statistical Literacy As the degrees of freedom...Ch. 8.2 - Critical Thinking Consider a 90% confidence...Ch. 8.2 - Critical Thinking Consider a 90% confidence...Ch. 8.2 - Critical Thinking Lorraine computed a confidence...Ch. 8.2 - Critical Thinking Lorraine was in a hum when she...Ch. 8.2 - Basic Computation: Confidence Interval Suppose x...Ch. 8.2 - Basic Computation: Confidence Interval A random...Ch. 8.2 - In Problems 13-19. assumethat the population of x...Ch. 8.2 - In Problems 13-19. assumethat the population of x...Ch. 8.2 - In Problems 13-19. assume that the population of x...Ch. 8.2 - In Problems 13-19, assume that the population of x...Ch. 8.2 - In Problems 13-19, assume that the population of x...Ch. 8.2 - In Problems 13-19, assume that the population of x...Ch. 8.2 - 19 Critical Thinking: Boxplots and Confidence...Ch. 8.2 - Crime Rale: Denver The following data represent...Ch. 8.2 - Finance: P/E Ratio The price of a share of stock...Ch. 8.2 - 22.
Baseball: Home Run Percentage The home run...Ch. 8.2 - Expand Your knowledge: Alternate Method for...Ch. 8.3 - Statistical Literacy For a binomial experiment...Ch. 8.3 - Statistical Literacy In order to use a normal...Ch. 8.3 - Critical Thinking Results of a poll of a random...Ch. 8.3 - Critical Thinking You want to conduct a survey to...Ch. 8.3 - Critical Thinking Jerry tested 30 laptop computers...Ch. 8.3 - Critical Thinking: Brain Teaser A requirement for...Ch. 8.3 - Basic Computation: Confidence Interval for p...Ch. 8.3 - Basic Computation: Confidence Interval for p...Ch. 8.3 - Basic Computation: Sample Size What is the minimal...Ch. 8.3 - Basic Computation: Sample Size What is the minimal...Ch. 8.3 - Myers-Briggs: Actors Isabel Myers was a pioneer in...Ch. 8.3 - Myers-Briggs: Judges In a random sample of 519...Ch. 8.3 - Navajo Lifestyle: Traditional Hogans A random...Ch. 8.3 - Archaeology: Pottery Santa Fe black-on-white is a...Ch. 8.3 - Health Care: Colorado Physicians A random sample...Ch. 8.3 - Law Enforcement: Escaped Convicts Case studies...Ch. 8.3 - Fishing: Barbless Hooks In a combined study of...Ch. 8.3 - Focus Problem: Trick or Treat In a survey of a...Ch. 8.3 - Marketing: Customer Loyalty In a marketing survey,...Ch. 8.3 - Marketing: Bargain Hunters In a marketing survey,...Ch. 8.3 - Lifestyle: Smoking In a survey of 1000 large...Ch. 8.3 - Opinion Poll: Crime and Violence A NewYork...Ch. 8.3 - Medical: Blood Type A random sample of medical...Ch. 8.3 - Business: Phone Contact How hard is it to reach a...Ch. 8.3 - Campus Life: Coeds What percentage of your campus...Ch. 8.3 - Small Business: Bankruptcy The National Council of...Ch. 8.3 - Prob. 27PCh. 8.3 - Expand Your Knowledge: Plus Four Confidence...Ch. 8 - Statist Literacy In your own words, carefully...Ch. 8 - Critical Thinking Suppose you are told that a 95%...Ch. 8 - Critical Thinking If you have a 99% confidence...Ch. 8 - For Problems 8-12, categorize each problem...Ch. 8 - For Problems 8-12, categorize each problem...Ch. 8 - Prob. 6CRCh. 8 - For Problems 8-12, categorize each problem...Ch. 8 - Prob. 8CRCh. 8 - Telephone Interviews: Survey The National Study of...Ch. 8 - Prob. 10CRCh. 8 - Prob. 11CRCh. 8 - Prob. 12CRCh. 8 - Expand Your Knowledge: Two Confidence Intervals...Ch. 8 - Garrison Bay is a small hay in Washington stale. A...Ch. 8 - Examine Figure 8-7. Fall Back " (a) Of the 1024...Ch. 8 - Examine Figure 8.-8, "Coupons: Limited Use." (a)...Ch. 8 - In this chapter, we have studied confidence...Ch. 8 - Throughout Chapter 8. we have used the normal...Ch. 8 - When the results of a survey or a poll are...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Exercise 4.2 Prove that, if A and B are independent, then so are A and B, Ac and B, and A and B.arrow_forward8. Show that, if {Xn, n ≥ 1) are independent random variables, then sup X A) < ∞ for some A.arrow_forward8- 6. Show that, for any random variable, X, and a > 0, 8 心 P(xarrow_forward15. This problem extends Problem 20.6. Let X, Y be random variables with finite mean. Show that 00 (P(X ≤ x ≤ Y) - P(X ≤ x ≤ X))dx = E Y — E X.arrow_forward(b) Define a simple random variable. Provide an example.arrow_forward17. (a) Define the distribution of a random variable X. (b) Define the distribution function of a random variable X. (c) State the properties of a distribution function. (d) Explain the difference between the distribution and the distribution function of X.arrow_forward16. (a) Show that IA(w) is a random variable if and only if A E Farrow_forward15. Let 2 {1, 2,..., 6} and Fo({1, 2, 3, 4), (3, 4, 5, 6}). (a) Is the function X (w) = 21(3, 4) (w)+711.2,5,6) (w) a random variable? Explain. (b) Provide a function from 2 to R that is not a random variable with respect to (N, F). (c) Write the distribution of X. (d) Write and plot the distribution function of X.arrow_forward20. Define the o-field R2. Explain its relation to the o-field R.arrow_forward7. Show that An → A as n→∞ I{An} - → I{A} as n→ ∞.arrow_forward7. (a) Show that if A,, is an increasing sequence of measurable sets with limit A = Un An, then P(A) is an increasing sequence converging to P(A). (b) Repeat the same for a decreasing sequence. (c) Show that the following inequalities hold: P (lim inf An) lim inf P(A) ≤ lim sup P(A) ≤ P(lim sup A). (d) Using the above inequalities, show that if A, A, then P(A) + P(A).arrow_forward19. (a) Define the joint distribution and joint distribution function of a bivariate ran- dom variable. (b) Define its marginal distributions and marginal distribution functions. (c) Explain how to compute the marginal distribution functions from the joint distribution function.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Statistics 4.1 Point Estimators; Author: Dr. Jack L. Jackson II;https://www.youtube.com/watch?v=2MrI0J8XCEE;License: Standard YouTube License, CC-BY
Statistics 101: Point Estimators; Author: Brandon Foltz;https://www.youtube.com/watch?v=4v41z3HwLaM;License: Standard YouTube License, CC-BY
Central limit theorem; Author: 365 Data Science;https://www.youtube.com/watch?v=b5xQmk9veZ4;License: Standard YouTube License, CC-BY
Point Estimate Definition & Example; Author: Prof. Essa;https://www.youtube.com/watch?v=OTVwtvQmSn0;License: Standard Youtube License
Point Estimation; Author: Vamsidhar Ambatipudi;https://www.youtube.com/watch?v=flqhlM2bZWc;License: Standard Youtube License