
Interpretation:
To show
To show the Jacobian matrix for the linearization has the form
Here, A and B are
By considering trace and determinant of matrix
To show that depending on the sizes of g and T, the determinant of matrix
By using computer, show that Hopf bifurcation can be supercritical.
Concept Introduction:
To find fixed point of the system, put
Jacobian matrix is used to check the stability of the fixed points, and it is given as:
The system which is settling down to equilibrium by exponentially damping and its decay rate depends on a control parameter
Answer to Problem 17E
Solution:
It is shown that the Jacobian matrix for the linearization has the form
It is shown that all eigenvalues of the matrix
It is shown that values of g and T determine whether the determinant of matrix
It is shown that the system goes through supercritical Hopf bifurcation.
Explanation of Solution
a)
The system equations are:
Assuming that
Here, the condition of
In above equation, L.H.S. and R.H.S. are zero and positive respectively when
Thus, the curves intersect and have unique symmetric solution.
b)
The Jacobian matrix is:
To prove determinant law,
Expanding along last column,
Again expanding along bottom row,
Therefore,
This result is used for calculation of eigenvalues of the
c)
Using determinant is product of the eigenvalues and trace is sum of eigenvalues,
But
Here,
From the above result,
The trace
Thus,
d)
For the matrix
The determinant
And trace
From the above results, the determinant is positive if
Trace can negative or positive depending upon values of b and T.
From the above conclusions of eigenvalues, pitchfork or Hopf bifurcation can occur at the point
By adjusting parameter g, if initially trace is negative, and by varying parameter g, its value is shifting towards positive value, then the pitchfork bifurcation occurs at
By adjusting parameter T, if the determinant is positive, by changing the parameter T, the trace of the matrix changes its sign, then the Hopf bifurcation occurs at a
e)
The plots of
For T being very small, the system is nearly settled down to fixed point

Increasing the value of T, the stable limit cycles just appear.

Further increasing the value of T, the size of the limit cycle increases.
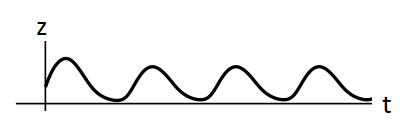
Therefore, the system goes through supercritical Hopf bifurcation.
Want to see more full solutions like this?
Chapter 8 Solutions
Nonlinear Dynamics and Chaos
- Which scatterplot shows a nonlinear association?arrow_forwardRamp metering is a traffic engineering idea that requires cars entering a freeway to stop for a certain period of time before joining the traffic flow. The theory is that ramp metering controls the number of cars on the freeway and the number of cars OA. Yes, there appears to be a high outlier in the Meters Off data. B. Yes, there appears to be a low outlier in the Meters On data. OC. Yes, there appears to be a high outlier in the Meters On data. OD. No, there does not appear to be any outliers. (b) Are the ramp meters effective in maintaining a higher speed on the freeway? Use the a=0.05 level of significance. State the null and alternative hypotheses. Choose the correct answer below. OA. Ho Hon Hoff H₁ Hon > Hoff OC. Ho Hon Hoff H₁ Hon Hoff # Determine the P-value for this test. *** P-value= (Round to three decimal places as needed.) OB. Ho Hon = Hoff H₁ Pon > Hoff O D. Ho Hon Hoff H₁-Hon > Hoff Choose the correct conclusion. O A. Do not reject Ho. There is sufficient evidence at the…arrow_forwardNeuroscience researchers examined the impact of environment on rat development. Rats were randomly assigned to be raised in one of the four following test conditions: Impoverished (wire mesh cage - housed alone), standard (cage with other rats), enriched (cage with other rats and toys), super enriched (cage with rats and toys changes on a periodic basis). After two months, the rats were tested on a variety of learning measures (including the number of trials to learn a maze to a three perfect trial criteria), and several neurological measure (overall cortical weight, degree of dendritic branching, etc.). The data for the maze task is below. Compute the appropriate test for the data provided below. Include solution. Thank youarrow_forward
- Ramp metering is a traffic engineering idea that requires cars entering a freeway to stop for a certain period of time before joining the traffic flow. The theory is that ramp metering controls the number of cars on the freeway and the number of cars accessing the freeway, resulting in a freer flow of cars, which ultimately results in faster travel times. To test whether ramp metering is effective in reducing travel times, engineers conducted an experiment in which a section of freeway had ramp meters installed on the on-ramps. The response variable for the study was speed of the vehicles. A random sample of 15 cars on the highway for a Monday at 6 p.m. with the ramp meters on and a second random sample of 15 cars on a different Monday at 6 pm with the meters off resulted in the following speeds (in miles per hour). (a) Uraw side-by-side Doxplots of each data set Does there appear to be a merence in the speeds? Are there any outlers? Choose the correct Dox plot below. A. 0 Off 15 30 45…arrow_forwarda.State the predictors available in this model.arrow_forwardNormally when you look at something, your left and right eyes take in very similar images, and your brain blends them together, However, if totally different images are shown to each eye, the brain does something wild: it perceives one image for a brief time, then switches again and again. To model this process, we posit that there are two populations of neurons with average firing rates x1 and x2. These two populations battle for dominance, resulting in a model for neuronal competition: x'1 = -x1 + F(I - bx2) x'2 = -x2 + F(I - bx1) Here F(x) = 1/(1 + e-x) is a "gain function", I > 0 is the strength of the input stimulus, and b > 0 is the strength of the antagonism between neuron groups. a) Show that the Jacobian at this symmetric fixed point has delta = 1 - b2(x* - (x*)2)2 and Tau = -2. Argue that for large enough b the stability of the fixed points ches from a stable node to a saddle. b) Does this model exhibit the binocular rivalry switching behavior observed in experiments?arrow_forward
 Calculus For The Life SciencesCalculusISBN:9780321964038Author:GREENWELL, Raymond N., RITCHEY, Nathan P., Lial, Margaret L.Publisher:Pearson Addison Wesley,
Calculus For The Life SciencesCalculusISBN:9780321964038Author:GREENWELL, Raymond N., RITCHEY, Nathan P., Lial, Margaret L.Publisher:Pearson Addison Wesley,
