
Concept explainers
Select a random sample of at least 30 individuals, and using the z test for proportions, test one or more of the following hypotheses. Use α = 0.05.
a. For educational level, H0: p = 0.50 for level 2.
b. For smoking status, H0: p = 0.20 for level 1.
c. For exercise level, H0: p = 0.10 for level 1.
d. For gender, H0: p = 0.50 for males.
a.
To test: The claim that
Answer to Problem 3DA
There is sufficient evidence to infer that the percentage for the education level of “college graduate” is not 0.50.
Explanation of Solution
Answer will vary. One of the possible answers is given below:
Given info:
A random sample of 100 individuals selected and found that 36 of them were college graduate.
Claim:
Calculation:
State the null and alternative hypotheses:
Null hypothesis:
Alternative hypothesis:
Test statistic value and P-value:
Software procedure:
Step by step procedure to obtain the test value using the MINITAB software:
- Choose Stat > Basic Statistics > 1 Proportion.
- Choose Summarized data.
- In Number of events, enter 36. In Number of trials, enter 100.
- Check Perform hypothesis test. In Hypothesized proportion, enter 0.50.
- Click Options. Under Alternative, and choose not equal.
- Click OK in each dialog box.
Output using the MINITAB software is given below:
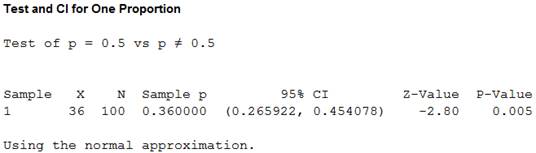
From the output, the test value is –2.80 and the P-value is 0.005.
Make the Decision:
Decision rule:
If
If
Here, the P-value is lesser than the level of significance.
That is,
By the decision rule, the null hypothesis is rejected.
Thus, the decision is “reject the null hypothesis”.
Summarize the result:
There is sufficient evidence to infer that the percentage for the education level of “college graduate” is not 0.50.
b.
To test: The claim that
Answer to Problem 3DA
There is sufficient evidence to infer that the percentage for the smoking status category of “Level 1: smoke less than one pack per day” is not 0.20.
Explanation of Solution
Given info:
A random sample of 100 individuals selected and found that 36 of them smoke less than one pack per day.
Claim:
Calculation:
State the null and alternative hypotheses:
Null hypothesis:
Alternative hypothesis:
Test statistic value and P-value:
Software procedure:
Step by step procedure to obtain the test value using the MINITAB software:
- Choose Stat > Basic Statistics > 1 Proportion.
- Choose Summarized data.
- In Number of events, enter 36. In Number of trials, enter 100.
- Check Perform hypothesis test. In Hypothesized proportion, enter 0.20.
- Click Options. Under Alternative, and choose not equal.
- Click OK in each dialog box.
Output using the MINITAB software is given below:
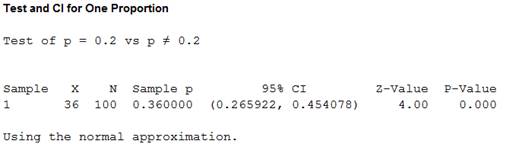
From the output, the test value is 4 and the P-value is 0.000.
Make the Decision:
Here, the P-value is lesser than the level of significance.
That is,
By the decision rule, the null hypothesis is rejected.
Thus, the decision is “reject the null hypothesis”.
Summarize the result:
There is sufficient evidence to infer that the percentage for the smoking status category of “Level 1: smoke less than one pack per day” is not 0.20.
c.
To test: The claim that
Answer to Problem 3DA
There is sufficient evidence to infer that the percentage for the exercise category “light” is not 0.10.
Explanation of Solution
Given info:
Claim:
Calculation:
State the null and alternative hypotheses:
Null hypothesis:
Alternative hypothesis:
Test statistic value and P-value:
Software procedure:
Step by step procedure to obtain the test value using the MINITAB software:
- Choose Stat > Basic Statistics > 1 Proportion.
- Choose Summarized data.
- In Number of events, enter 38. In Number of trials, enter 100.
- Check Perform hypothesis test. In Hypothesized proportion, enter 0.10.
- Click Options. Under Alternative, and choose not equal.
- Click OK in each dialog box.
Output using the MINITAB software is given below:
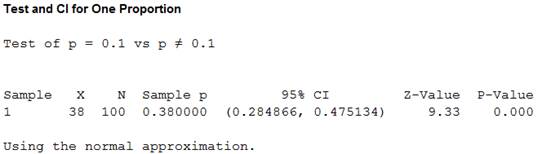
From the output, the test value is 9.33 and the P-value is 0.000.
Make the Decision:
Here, the P-value is lesser than the level of significance.
That is,
By the decision rule, the null hypothesis is rejected.
Thus, the decision is “reject the null hypothesis”.
Summarize the result:
There is sufficient evidence to infer that the percentage for the exercise category “light” is not 0.10.
d.
To test: The claim that
Answer to Problem 3DA
There is sufficient evidence to infer that the percentage for male is 0.50.
Explanation of Solution
Given info:
The total number of individual is 100 and the number of male is 50.
Claim:
Calculation:
State the null and alternative hypotheses:
Null hypothesis:
Alternative hypothesis:
Test statistic value and P-value:
Software procedure:
Step by step procedure to obtain the test value using the MINITAB software:
- Choose Stat > Basic Statistics > 1 Proportion.
- Choose Summarized data.
- In Number of events, enter 50. In Number of trials, enter 100.
- Check Perform hypothesis test. In Hypothesized proportion, enter 0.50.
- Click Options. Under Alternative, and choose not equal.
- Click OK in each dialog box.
Output using the MINITAB software is given below:
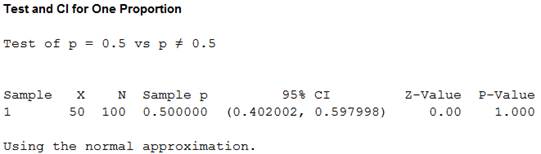
From the output, the test value is 0 and the P-value is 1.
Make the Decision:
Here, the P-value is greater than the level of significance.
That is,
By the decision rule, the null hypothesis is not rejected.
Thus, the decision is “fail to reject the null hypothesis”.
Summarize the result:
There is sufficient evidence to infer that the percentage for male is 0.50.
Want to see more full solutions like this?
Chapter 8 Solutions
ELEMENTARY STATISTICS >C<
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning

