Chapter 7.CT, Problem 1CT

Draw and describe the locus of points in the plane that are equidistant from parallel lines l and m.

_________________________________________

________________________________________

To determine

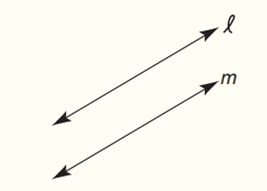
To draw and describe:

The locus of points in the plane that are equidistant from parallel lines l and m.

Answer to Problem 1CT

Solution:

The locus is in between both lines and is parallel to both.

Explanation of Solution

Definition:

A locus is set of all points and only those points that satisfy a given condition or set of conditions.

In must be noted that, the phrase “all points and only those points” has dual meaning as follows:

1. All points of the locus satisfy the given condition.

2. All points satisfying the given locus conditions are included in the locus.

Calculation:

A locus maintains an equal distance from each line.

Thus, we obtain that the locus must be half way between the two lines. In addition, since it maintains a constant distance, it must be parallel to both.

From this we came to know that the locus equidistant from two parallel lines l and m, is a line parallel to both l and m and halfway between them.

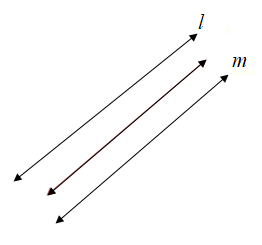
Conclusion:

The path formed by all points the same distance from two parallel lines will be one line halfway between the parallel lines.