EBK MATHEMATICS FOR MACHINE TECHNOLOGY
8th Edition
ISBN: 9781337798396
Author: SMITH
Publisher: CENGAGE LEARNING - CONSIGNMENT
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 73, Problem 48AR
To determine
(a)
The length of side m.
Expert Solution
Answer to Problem 48AR
The length of side AC is m=8.484 inches
Explanation of Solution
Given information:
The given figure is
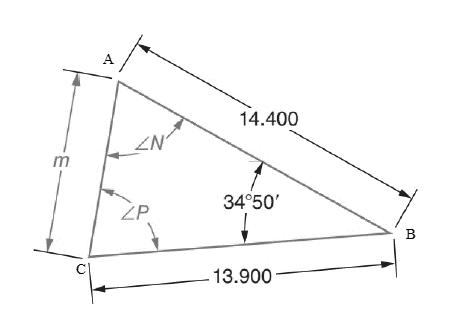
Calculation:
Let us consider the triangle ABC, the length of side AC of length m can be found from cosine law. In triangle ABC,
AC2=AB2+BC2−2×AB×BC×cosBAC2=14.4002+13.9002−2×14.4×13.9×cos34°50'AC2=207.36+193.21−324.589AC2=71.98AC=√71.98=mm=8.484
m=8.484 inches
Conclusion:
Thus, the length of side AC is m=8.484 inches
To determine
(b)
The value of ∠N.
Expert Solution
Answer to Problem 48AR
The value of angle N is ∠N=69.36°
Explanation of Solution
Given information:
The given figure is
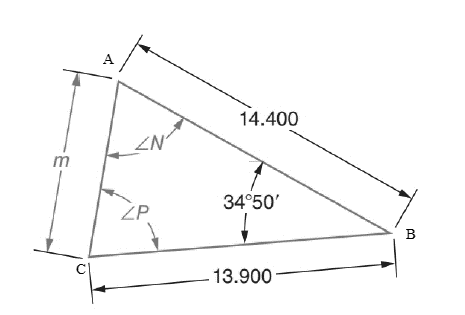
Calculation:
Let us consider the triangle ABC, the value of angle N can be found from sine law. In triangle ABC,
From the calculated value of side AC ( m=8.484 inches ),
sinABC=sinBAC=sinCABsin∠N13.900=sin34°50'8.484=sin∠P14.4
sin∠N13.900=sin34°50'8.484sin∠N=sin34°50'8.484×13.900sin∠N=0.9358∠N=sin−1(0.9358)∠N=69.36°
∠N=69.36°
Conclusion:
Thus, the value of angle N is ∠N=69.36°.
To determine
(c)
The value of ∠P.
Expert Solution
Answer to Problem 48AR
The value of angle P is ∠P=75°48'
Explanation of Solution
Given information:
The given figure is
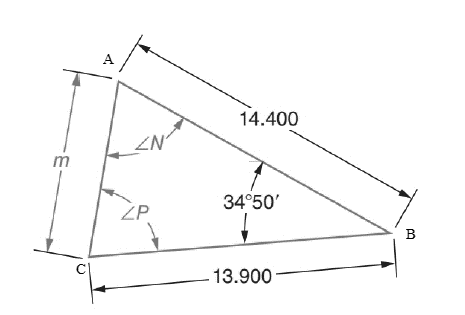
Calculation:
Let us consider the triangle ABC, the value of angle P can be found from sine law. In triangle ABC,
From the calculated value of side AC ( m=8.484 inches ),
sinABC=sinBAC=sinCABsin∠N13.900=sin34°50'8.484=sin∠P14.4
sin34°50'8.484=sin∠P14.4sin∠P=sin34°50'8.484×14.4sin∠P=0.9694∠P=sin−1(0.9694)∠P=75.81°∠P=75°48'
∠P=75°48'
Conclusion:
Thus, the value of angle P is ∠P=75°48'.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Definition: A topology on a set X is a collection T of subsets of X having the following
properties.
(1) Both the empty set and X itself are elements of T.
(2) The union of an arbitrary collection of elements of T is an element of T.
(3) The intersection of a finite number of elements of T is an element of T.
A set X with a specified topology T is called a topological space. The subsets of X that are
members of are called the open sets of the topological space.
2) Prove that
for all integers n > 1.
dn 1
(2n)!
1
=
dxn 1
- Ꮖ 4 n! (1-x)+/
Definition: A topology on a set X is a collection T of subsets of X having the following
properties.
(1) Both the empty set and X itself are elements of T.
(2) The union of an arbitrary collection of elements of T is an element of T.
(3) The intersection of a finite number of elements of T is an element of T.
A set X with a specified topology T is called a topological space. The subsets of X that are
members of are called the open sets of the topological space.
Chapter 73 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
Ch. 73 - With reference 1, name the sides of each of the...Ch. 73 - With reference to 1, name the sides of each of the...Ch. 73 - Prob. 3ARCh. 73 - Prob. 4ARCh. 73 - Prob. 5ARCh. 73 - Prob. 6ARCh. 73 - Prob. 7ARCh. 73 - Prob. 8ARCh. 73 - Prob. 9ARCh. 73 - Prob. 10AR
Ch. 73 - Prob. 11ARCh. 73 - Prob. 12ARCh. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in decimal degree to 2...Ch. 73 - Determine the values A in decimal degree to 2...Ch. 73 - Determine the values A in decimal degree to 2...Ch. 73 - For each of the following functions of angles,...Ch. 73 - For each of the following functions of angles,...Ch. 73 - For each of the following functions of angles,...Ch. 73 - For each of the following functions of angles,...Ch. 73 - Solve the following exercises. Compute angles to...Ch. 73 - Solve the following exercises. Compute angles to...Ch. 73 - Solve the following exercises. Compute angles to...Ch. 73 - Prob. 29ARCh. 73 - Prob. 30ARCh. 73 - Prob. 31ARCh. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Prob. 40ARCh. 73 - Prob. 41ARCh. 73 - Prob. 42ARCh. 73 - Prob. 43ARCh. 73 - Prob. 44ARCh. 73 - Prob. 45ARCh. 73 - Prob. 46ARCh. 73 - Prob. 47ARCh. 73 - Prob. 48ARCh. 73 - Prob. 49ARCh. 73 - Determine the sine, cosine, tangent, cotangent,...Ch. 73 - Determine the sine, cosine, tangent, cotangent,...Ch. 73 - Prob. 52ARCh. 73 - Prob. 53ARCh. 73 - Determine the sine, cosine, tangent, cotangent,...Ch. 73 - Prob. 55ARCh. 73 - Prob. 56AR
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Definition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward3) Let a1, a2, and a3 be arbitrary real numbers, and define an = 3an 13an-2 + An−3 for all integers n ≥ 4. Prove that an = 1 - - - - - 1 - - (n − 1)(n − 2)a3 − (n − 1)(n − 3)a2 + = (n − 2)(n − 3)aı for all integers n > 1.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward
- Definition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward1) If f(x) = g¹ (g(x) + a) for some real number a and invertible function g, show that f(x) = (fo fo... 0 f)(x) = g¯¹ (g(x) +na) n times for all integers n ≥ 1.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Fundamental Trigonometric Identities: Reciprocal, Quotient, and Pythagorean Identities; Author: Mathispower4u;https://www.youtube.com/watch?v=OmJ5fxyXrfg;License: Standard YouTube License, CC-BY