
In Problems 17 to 20, find the Fourier sine transform of the function in the indicated problem, and write
Problem 10.
In Problems 3 to 12, find the exponential Fourier transform of the given
10.
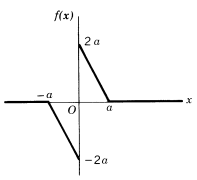
Want to see the full answer?
Check out a sample textbook solution
Chapter 7 Solutions
Mathematical Methods in the Physical Sciences
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
STATISTICS F/BUSINESS+ECONOMICS-TEXT
A First Course in Probability (10th Edition)
Algebra and Trigonometry (6th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Calculus: Early Transcendentals (2nd Edition)
- For a function to have an inverse, it must be ___________. To define the inverse sine function, we restrict the ____________ of the sine function to the interval ____________.arrow_forwardKk.342. If sin\theta =-(1)/(2) and 3\pi <\theta <(7\pi )/(2), thenarrow_forwardExpand sin(50) in powers of sin(0) and cos(0).arrow_forward
- 4. Express the function f (x) = 11 sin x + 7 cos x as a function in terms of sine. Express your answer in degrees. Round to 2 decimal places.arrow_forwardFor the following function, you are given one period of the function. = sin tx on the interval - 2arrow_forwardA calculator may be used on the following questions. Air is being pumped into a spherical balloon at the rate of R(t)=t+cos(t-1) cm³/min, but there is a small hole in the balloon and at the same time air is leaking out at the rate of L(t) = 0.5 tan-¹(t) cm³/min. = -2 144 12+ 10+ 8 6 2 Select one: O a. 17 ~ 2 C. ++ 4 1/10 110. 0 6 Which of the following is true for 0 ≤t≤ 10, where t is measured in minutes? +00 8 10 + 12 X minutes. O b. R(0) - L(0) = 1 -10 R(t)- L (t) dt represents the increase in volume during the first 10 minutes. R(t) L(t)dt represents the increase in volume each minute during the first 10 10 O d. [ R(t)-I(t)dr represents the volume of the balloon after the first 10 minutes. 0arrow_forwardarrow_back_iosarrow_forward_ios
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning


