
Linear Algebra with Applications (2-Download)
5th Edition
ISBN: 9780321796974
Author: Otto Bretscher
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 7.1, Problem 24E
In Exercises 24 through 29, consider a dynamical system
→x(t+1)=A→x(t)
with two components. The accompanying sketch shows the initial state
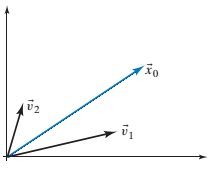
24.
λ1=1.1,λ2=0.9
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
part 3 of the question is:
A power outage occurs 6 min after the ride started. Passengers must wait for their cage to be manually cranked into the lowest position in order to exit the ride. Sine function model: where h is the height of the last passenger above the ground measured in feet and t is the time of operation of the ride in minutes.
What is the height of the last passenger at the moment of the power outage? Verify your answer by evaluating the sine function model.
Will the last passenger to board the ride need to wait in order to exit the ride? Explain.
2. The duration of the ride is 15 min.
(a) How many times does the last passenger who boarded the ride make a complete loop on the Ferris
wheel?
(b) What is the position of that passenger when the ride ends?
3. A scientist recorded the movement of a pendulum for 10 s. The scientist began recording when the pendulum
was at its resting position. The pendulum then moved right (positive displacement) and left (negative
displacement) several times. The pendulum took 4 s to swing to the right and the left and then return to its
resting position. The pendulum's furthest distance to either side was 6 in. Graph the function that represents
the pendulum's displacement as a function of time.
Answer:
f(t)
(a) Write an equation to represent the displacement of the pendulum as a function of time.
(b) Graph the function.
10
9
8
7
6
5
4
3
2
1
0
t
1
2
3
4
5
6
7
8
9 10
11
12
13 14
15
-1
-5.
-6
-7
-8
-9
-10-
Chapter 7 Solutions
Linear Algebra with Applications (2-Download)
Ch. 7.1 - In Exercises 1 through 4, let A be an invertible...Ch. 7.1 - In Exercises 1 through 4, let A be an invertible...Ch. 7.1 - In Exercises 1 through 4, let A be an invertible...Ch. 7.1 - In Exercises 1 through 4, let A be an invertible...Ch. 7.1 - If a vector is an eigenvector of both A and B, is...Ch. 7.1 - If a vector is an eigenvector of both A and B, is...Ch. 7.1 - If a vector is an eigenvector of the nnmatrixA...Ch. 7.1 - Find all 22 matrix for which e1=[10] is an...Ch. 7.1 - Find all 22 matrix for which e1 is an eigenvector.Ch. 7.1 - Find all 22 matrix for which [12] is an...
Ch. 7.1 - Find all 22 matrix for which [23] is an...Ch. 7.1 - Consider the matrix A=[2034] . Show that 2 and 4...Ch. 7.1 - Show that 4 is an eigenvalue of A=[661513] and...Ch. 7.1 - Find all 44 matrices for which e2 is an...Ch. 7.1 - Arguing geometrically, find all eigenvectors and...Ch. 7.1 - Arguing geometrically, find all eigenvectors and...Ch. 7.1 - Arguing geometrically, find all eigenvectors and...Ch. 7.1 - Arguing geometrically, find all eigenvectors and...Ch. 7.1 - Arguing geometrically, find all eigenvectors and...Ch. 7.1 - Arguing geometrically, find all eigenvectors and...Ch. 7.1 - Arguing geometrically, find all eigenvectors and...Ch. 7.1 - Arguing geometrically, find all eigenvectors and...Ch. 7.1 - Use matrix products to prove the following: If...Ch. 7.1 - In Exercises 24 through 29, consider a dynamical...Ch. 7.1 - In Exercises 24 through 29, consider a dynamical...Ch. 7.1 - In Exercises 24 through 29, consider a dynamical...Ch. 7.1 - In Exercises 24 through 29, consider a dynamical...Ch. 7.1 - In Exercises 24 through 29, consider a dynamical...Ch. 7.1 - In Exercises 24 through 29, consider a dynamical...Ch. 7.1 - In Exercises 30 through 32, consider the dynamical...Ch. 7.1 - In Exercises 30 through 32, consider the dynamical...Ch. 7.1 - In Exercises 30 through 32, consider the dynamical...Ch. 7.1 - Find a 22 matrix A such that x(t)=[ 2 t 6 t 2 t+ 6...Ch. 7.1 - Suppose is an eigenvector of the nn matrix A,with...Ch. 7.1 - Show that similar matrices have the same...Ch. 7.1 - Find a 22 matrix A such that [31] and [12] are...Ch. 7.1 - Consider the matrix A=[3443] a. Use the geometric...Ch. 7.1 - We are told that [111] is an eigenvector of the...Ch. 7.1 - Find a basis of the linear space V of all 22...Ch. 7.1 - Find a basis of the linear space V of all 22...Ch. 7.1 - Find a basis of the linear space V of all 22...Ch. 7.1 - Find a basis of the linear space V of all 33...Ch. 7.1 - Consider the linear space V of all nn matrices for...Ch. 7.1 - For nn , find the dimension of the space of all nn...Ch. 7.1 - If is any nonzero vector in 2 , what is the...Ch. 7.1 - If is an eigenvector of matrix A with associated...Ch. 7.1 - If is an eigenvector of matrix A, show that is...Ch. 7.1 - If A is a matrix of rank 1, show that any nonzero...Ch. 7.1 - Give an example of a matrix A of rank 1 that fails...Ch. 7.1 - Find an eigenbasis for each of the matrices A in...Ch. 7.1 - Find an eigenbasis for each of the matrices A in...Ch. 7.1 - Find an eigenbasis for each of the matrices A in...Ch. 7.1 - Find an eigenbasis for each of the matrices A in...Ch. 7.1 - Find an eigenbasis for each of the matrices A in...Ch. 7.1 - Arguing geometrically, find an eigenbasis for each...Ch. 7.1 - Arguing geometrically, find an eigenbasis for each...Ch. 7.1 - Arguing geometrically, find an eigenbasis for each...Ch. 7.1 - Arguing geometrically, find an eigenbasis for each...Ch. 7.1 - Arguing geometrically, find an eigenbasis for each...Ch. 7.1 - Arguing geometrically, find an eigenbasis for each...Ch. 7.1 - Arguing geometrically, find an eigenbasis for each...Ch. 7.1 - Arguing geometrically, find an eigenbasis for each...Ch. 7.1 - Arguing geometrically, find an eigenbasis for each...Ch. 7.1 - In all parts of this problem, let V be the linear...Ch. 7.1 - Consider an nn matrix A. A subspace V of n is...Ch. 7.1 - a. Give an example of a 33 matrix A with as many...Ch. 7.1 - Consider the coyotesroadrunner system discussed...Ch. 7.1 - Two interacting populations of hares and foxes can...Ch. 7.1 - Two interacting populations of coyotes and...Ch. 7.1 - Imagine that you are diabetic and have to pay...Ch. 7.1 - Three holy men (let’s call them Anselm, Benjamin,...Ch. 7.1 - Consider the growth of a lilac bush. The state of...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - For each of the matrices in Exercises 1 through...Ch. 7.2 - Consider a 44 matrix A=[BC0D] , where B, C, and D...Ch. 7.2 - Consider the matrix A=[1k11] , where k is an...Ch. 7.2 - Consider the matrix A=[abbc] , where a, b, and c...Ch. 7.2 - Consider the matrix A=[abba] , where a andb are...Ch. 7.2 - Consider the matrix A=[abba] , where a andb...Ch. 7.2 - True or false? If the determinant of a 22 matrix A...Ch. 7.2 - Ifa 22 matrix A has two distinct eigenvalues 1 and...Ch. 7.2 - Prove the part of Theorem 7.2.8 that concerns the...Ch. 7.2 - Consider an arbitrary nn matrix A. What is...Ch. 7.2 - Suppose matrix A is similar to B. What is the...Ch. 7.2 - Find all eigenvalues of the positive transition...Ch. 7.2 - Consider a positive transition matrix A=[abcd] ,...Ch. 7.2 - Based on your answers in Exercises 24 and 25,...Ch. 7.2 - a. Based on your answers in Exercises 24 and 25,...Ch. 7.2 - Consider the isolated Swiss town of Andelfingen,...Ch. 7.2 - Consider an nn matrix A such that the sum of the...Ch. 7.2 - In all parts of this problem, consider an nn...Ch. 7.2 - Consider a positive transition matrix A. Explain...Ch. 7.2 - Consider the matrix A=[010001k30] wherek is an...Ch. 7.2 - a. Find the characteristic polynomial of the...Ch. 7.2 - Prob. 34ECh. 7.2 - Give an example of a 44 matrix A without real...Ch. 7.2 - For an arbitrary positive integer n, give a...Ch. 7.2 - Prob. 37ECh. 7.2 - IfA isa 22 matrixwith trA=5 and detA=14 ,what are...Ch. 7.2 - Prob. 39ECh. 7.2 - Prob. 40ECh. 7.2 - Prob. 41ECh. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.2 - For which value of the constant k does the matrix...Ch. 7.2 - In all the parts of this problem, consider a...Ch. 7.2 - Prob. 47ECh. 7.2 - Prob. 48ECh. 7.2 - Prob. 49ECh. 7.2 - Prob. 50ECh. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - Prob. 9ECh. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - Prob. 11ECh. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - Prob. 15ECh. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - Prob. 17ECh. 7.3 - Prob. 18ECh. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - For each of the matrices A in Exercises 1 through...Ch. 7.3 - Find a 22 matrix A for which E1=span[12] and...Ch. 7.3 - Find a 22 matrix A for which E7=2 .Ch. 7.3 - Find all eigenvalues and eigenvectors of A=[1101]...Ch. 7.3 - Find a 22 matrix A for which E1=span[21] is the...Ch. 7.3 - What can you say about the geometric multiplicity...Ch. 7.3 - Show that if a 66 matrix A has a negative...Ch. 7.3 - Consider a 22 matrix A. Suppose that trA=5 and...Ch. 7.3 - Consider the matrix Jn(k)=[000000000k10000k] (with...Ch. 7.3 - Consider a diagonal nn matrix A with rank A=rn ....Ch. 7.3 - Consider an upper triangular nn matrix A with aii0...Ch. 7.3 - Suppose there is an eigenbasis for a matrix A....Ch. 7.3 - Prob. 32ECh. 7.3 - Prob. 33ECh. 7.3 - Suppose that B=S1AS for some nn matrices A, B, and...Ch. 7.3 - Is matrix [1203] similar to [3012] ?Ch. 7.3 - Is matrix [0153] similar to [1243] ?Ch. 7.3 - Consider a symmetric nn matrix A. Show that if ...Ch. 7.3 - Consider a rotation T(x)=Ax in 3 . (That is, A is...Ch. 7.3 - Consider a subspace V of n with dim(V)=m . a....Ch. 7.3 - For which values of constants a, b, and c are the...Ch. 7.3 - Prob. 41ECh. 7.3 - For which values of constants a, b, and c are the...Ch. 7.3 - Prob. 43ECh. 7.3 - For which values of constants a, b, and c are the...Ch. 7.3 - For which values of constants a, b, and c are the...Ch. 7.3 - Prob. 46ECh. 7.3 - For which values of constants a, b, and c are the...Ch. 7.3 - For which values of constants a, b, and c are the...Ch. 7.3 - Prob. 49ECh. 7.3 - For which values of constants a, b, and c are the...Ch. 7.3 - Prob. 51ECh. 7.3 - Find the characteristic polynomial of the nn...Ch. 7.3 - Prob. 53ECh. 7.3 - Prob. 54ECh. 7.3 - Give an example of a 33 matrix A with nonzero...Ch. 7.3 - Prob. 56ECh. 7.4 - For the matrices A in Exercises 1 through 12, find...Ch. 7.4 - For the matrices A in Exercises 1 through 12, find...Ch. 7.4 - Prob. 3ECh. 7.4 - For the matrices A in Exercises 1 through 12, find...Ch. 7.4 - For the matrices A in Exercises 1 through 12, find...Ch. 7.4 - Prob. 6ECh. 7.4 - Prob. 7ECh. 7.4 - Prob. 8ECh. 7.4 - Prob. 9ECh. 7.4 - Prob. 10ECh. 7.4 - Prob. 11ECh. 7.4 - Prob. 12ECh. 7.4 - Prob. 13ECh. 7.4 - For the matrices A and the vectorsx0in Exercises...Ch. 7.4 - Prob. 15ECh. 7.4 - Prob. 16ECh. 7.4 - Prob. 17ECh. 7.4 - For the matrices A and the vectorsx0in Exercises...Ch. 7.4 - Prob. 19ECh. 7.4 - For the matrices A in Exercises 20 through 24,...Ch. 7.4 - For the matrices A in Exercises 20 through 24,...Ch. 7.4 - Prob. 22ECh. 7.4 - Prob. 23ECh. 7.4 - Prob. 24ECh. 7.4 - Prob. 25ECh. 7.4 - Prob. 26ECh. 7.4 - Prob. 27ECh. 7.4 - Prob. 28ECh. 7.4 - Prob. 29ECh. 7.4 - a. Sketch a phase portrait for the dynamical...Ch. 7.4 - Let x(t) and y(t) be the annual defense budgets of...Ch. 7.4 - Prob. 32ECh. 7.4 - Prob. 33ECh. 7.4 - In an unfortunate accident involving an Austrian...Ch. 7.4 - Prob. 35ECh. 7.4 - A machine contains the grid of wires shown in the...Ch. 7.4 - Prob. 37ECh. 7.4 - Prob. 38ECh. 7.4 - Find all the eigenvalues and “eigenvectors” of the...Ch. 7.4 - Prob. 40ECh. 7.4 - Prob. 41ECh. 7.4 - Prob. 42ECh. 7.4 - Prob. 43ECh. 7.4 - Find all the eigenvalues and “eigenvectors” of the...Ch. 7.4 - Find all the eigenvalues and “eigenvectors” of the...Ch. 7.4 - Prob. 46ECh. 7.4 - Prob. 47ECh. 7.4 - Find all the eigenvalues and “eigenvectors” of the...Ch. 7.4 - Prob. 49ECh. 7.4 - Prob. 50ECh. 7.4 - Find all the eigenvalues and “eigenvectors” of the...Ch. 7.4 - Prob. 52ECh. 7.4 - For a regular transition matrix A, prove the...Ch. 7.4 - Prob. 54ECh. 7.4 - Prob. 55ECh. 7.4 - Prob. 56ECh. 7.4 - Consider an mn matrix A and an nm matrix B. Using...Ch. 7.4 - Prob. 58ECh. 7.4 - Prob. 59ECh. 7.4 - Prob. 60ECh. 7.4 - Prob. 61ECh. 7.4 - Prob. 62ECh. 7.4 - Consider the linear transformation T(f)=f from C...Ch. 7.4 - Prob. 64ECh. 7.4 - Prob. 65ECh. 7.4 - Prob. 66ECh. 7.4 - Consider a 55 matrix A with two distinct...Ch. 7.4 - Prob. 68ECh. 7.4 - We say that two n x n matrices A and B are...Ch. 7.4 - Prob. 70ECh. 7.4 - Prob. 71ECh. 7.4 - Prob. 72ECh. 7.4 - Prove the CayleyHamilton theorem, fA(A)=0 , for...Ch. 7.4 - Prob. 74ECh. 7.5 - Write the complex number z=33i in polar form.Ch. 7.5 - Find all complex numbers z such that z4=1 ....Ch. 7.5 - Prob. 3ECh. 7.5 - Prob. 4ECh. 7.5 - Prob. 5ECh. 7.5 - If z is a nonzero complex number in polar form,...Ch. 7.5 - Prob. 7ECh. 7.5 - Prob. 8ECh. 7.5 - Prob. 9ECh. 7.5 - Prove the fundamental theorem of algebra for cubic...Ch. 7.5 - Prob. 11ECh. 7.5 - Consider a polynomial f() with real coefficients....Ch. 7.5 - For the matrices A listed in Exercises 13 through...Ch. 7.5 - For the matrices A listed in Exercises 13 through...Ch. 7.5 - For the matrices A listed in Exercises 13 through...Ch. 7.5 - For the matrices A listed in Exercises 13 through...Ch. 7.5 - For the matrices A listed in Exercises 13 through...Ch. 7.5 - Prob. 18ECh. 7.5 - Prob. 19ECh. 7.5 - Find all complex eigenvalues of the matrices in...Ch. 7.5 - Find all complex eigenvalues of the matrices in...Ch. 7.5 - Prob. 22ECh. 7.5 - Find all complex eigenvalues of the matrices in...Ch. 7.5 - Find all complex eigenvalues of the matrices in...Ch. 7.5 - Prob. 25ECh. 7.5 - Prob. 26ECh. 7.5 - Suppose a real 33 matrix A has only two distinct...Ch. 7.5 - Suppose a 33 matrix A has the real eigenvalue 2...Ch. 7.5 - Prob. 29ECh. 7.5 - a. If 2i is an eigenvalue of a real 22 matrix A,...Ch. 7.5 - Prob. 31ECh. 7.5 - Prob. 32ECh. 7.5 - Prob. 33ECh. 7.5 - Exercise 33 illustrates how you can use the powers...Ch. 7.5 - Demonstrate the formula trA=1+2+...+n . where the...Ch. 7.5 - In 1990, the population of the African country...Ch. 7.5 - Prob. 37ECh. 7.5 - Prob. 38ECh. 7.5 - Prob. 39ECh. 7.5 - Prob. 40ECh. 7.5 - Prob. 41ECh. 7.5 - Prob. 42ECh. 7.5 - Prob. 43ECh. 7.5 - Prob. 44ECh. 7.5 - Prob. 45ECh. 7.5 - Prob. 46ECh. 7.5 - Prob. 47ECh. 7.5 - Prob. 48ECh. 7.5 - Prob. 49ECh. 7.5 - Prob. 50ECh. 7.5 - Prob. 51ECh. 7.5 - Prob. 52ECh. 7.5 - Prob. 53ECh. 7.5 - Prob. 54ECh. 7.5 - Prob. 55ECh. 7.6 - For the matrices A in Exercises 1 through 10,...Ch. 7.6 - Prob. 2ECh. 7.6 - Prob. 3ECh. 7.6 - Prob. 4ECh. 7.6 - For the matrices A in Exercises 1 through 10,...Ch. 7.6 - Prob. 6ECh. 7.6 - Prob. 7ECh. 7.6 - Prob. 8ECh. 7.6 - For the matrices A in Exercises 1 through 10,...Ch. 7.6 - Prob. 10ECh. 7.6 - Consider the matrices A in Exercises 11 through...Ch. 7.6 - Prob. 12ECh. 7.6 - Prob. 13ECh. 7.6 - Prob. 14ECh. 7.6 - Prob. 15ECh. 7.6 - Prob. 16ECh. 7.6 - For the matrices A in Exercises 17 through 24,...Ch. 7.6 - For the matrices A in Exercises 17 through 24,...Ch. 7.6 - Prob. 19ECh. 7.6 - For the matrices A in Exercises 17 through 24,...Ch. 7.6 - For the matrices A in Exercises 17 through 24,...Ch. 7.6 - For the matrices A in Exercises 17 through 24,...Ch. 7.6 - Prob. 23ECh. 7.6 - Prob. 24ECh. 7.6 - Prob. 25ECh. 7.6 - Prob. 26ECh. 7.6 - Prob. 27ECh. 7.6 - Prob. 28ECh. 7.6 - Consider an invertiblennmatrix A such that the...Ch. 7.6 - Prob. 30ECh. 7.6 - Prob. 31ECh. 7.6 - Prob. 32ECh. 7.6 - Prob. 33ECh. 7.6 - Consider a dynamical system x(t+1)=Ax(t) , whereA...Ch. 7.6 - Prob. 35ECh. 7.6 - Prob. 36ECh. 7.6 - Prob. 37ECh. 7.6 - Prob. 38ECh. 7.6 - Prob. 39ECh. 7.6 - Consider the matrix A=[pqrsqpsrrspqsrqp] , wherep,...Ch. 7.6 - Prob. 41ECh. 7.6 - Prob. 42ECh. 7 - If 0 is an eigenvalue of a matrix A, then detA=0 .Ch. 7 - Prob. 2ECh. 7 - Prob. 3ECh. 7 - Prob. 4ECh. 7 - The algebraic multiplicity of an eigenvalue cannot...Ch. 7 - Prob. 6ECh. 7 - Prob. 7ECh. 7 - Prob. 8ECh. 7 - There exists a diagonalizable 55 matrix with only...Ch. 7 - Prob. 10ECh. 7 - Prob. 11ECh. 7 - Prob. 12ECh. 7 - Prob. 13ECh. 7 - If Ais a noninvertible nn matrix, then the...Ch. 7 - If matrix A is diagonalizable, then its transpose...Ch. 7 - Prob. 16ECh. 7 - Prob. 17ECh. 7 - If A andB are nn matrices, if is an eigenvalue...Ch. 7 - Prob. 19ECh. 7 - Prob. 20ECh. 7 - Prob. 21ECh. 7 - Prob. 22ECh. 7 - Prob. 23ECh. 7 - Prob. 24ECh. 7 - Prob. 25ECh. 7 - Prob. 26ECh. 7 - Prob. 27ECh. 7 - Prob. 28ECh. 7 - Prob. 29ECh. 7 - Prob. 30ECh. 7 - Prob. 31ECh. 7 - If a 44 matrix A is diagonalizable, then the...Ch. 7 - Prob. 33ECh. 7 - Prob. 34ECh. 7 - Prob. 35ECh. 7 - Prob. 36ECh. 7 - Prob. 37ECh. 7 - Prob. 38ECh. 7 - IfAisa22 matrixsuch that trA=1 and detA=6 , then A...Ch. 7 - If a matrix is diagonalizable, then the algebraic...Ch. 7 - Prob. 41ECh. 7 - Prob. 42ECh. 7 - Prob. 43ECh. 7 - Prob. 44ECh. 7 - Prob. 45ECh. 7 - Prob. 46ECh. 7 - Prob. 47ECh. 7 - Prob. 48ECh. 7 - Prob. 49ECh. 7 - Prob. 50ECh. 7 - Prob. 51ECh. 7 - Prob. 52ECh. 7 - Prob. 53ECh. 7 - Prob. 54ECh. 7 - Prob. 55ECh. 7 - Prob. 56ECh. 7 - Prob. 57ECh. 7 - Prob. 58E
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- A power outage occurs 6 min after the ride started. Passengers must wait for their cage to be manually cranked into the lowest position in order to exit the ride. Sine function model: h = −82.5 cos (3πt) + 97.5 where h is the height of the last passenger above the ground measured in feet and t is the time of operation of the ride in minutes. (a) What is the height of the last passenger at the moment of the power outage? Verify your answer by evaluating the sine function model. (b) Will the last passenger to board the ride need to wait in order to exit the ride? Explain.arrow_forwardThe Colossus Ferris wheel debuted at the 1984 New Orleans World's Fair. The ride is 180 ft tall, and passengers board the ride at an initial height of 15 ft above the ground. The height above ground, h, of a passenger on the ride is a periodic function of time, t. The graph displays the height above ground of the last passenger to board over the course of the 15 min ride. Height of Passenger in Ferris Wheel 180 160 140- €120 Height, h (ft) 100 80 60 40 20 0 ך 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Time of operation, t (min) Sine function model: h = −82.5 cos (3πt) + 97.5 where h is the height of the passenger above the ground measured in feet and t is the time of operation of the ride in minutes. What is the period of the sine function model? Interpret the period you found in the context of the operation of the Ferris wheel. Answer:arrow_forward1. Graph the function f(x)=sin(x) −2¸ Answer: y -2π 一元 1 −1 -2 -3 -4+ 元 2πarrow_forward
- 3. Graph the function f(x) = −(x-2)²+4 Answer: f(x) 6 5 4 3 2+ 1 -6-5 -4-3-2-1 × 1 2 3 4 5 6 -1 -2+ ရာ -3+ -4+ -5 -6arrow_forward2. Graph the function f(x) = cos(2x)+1 Answer: -2π 一元 y 3 2- 1 -1 -2+ ရာ -3- Π 2πarrow_forward2. Graph the function f(x) = |x+1+2 Answer: -6-5-4-3-2-1 f(x) 6 5 4 3 2 1 1 2 3 4 5 6 -1 -2 -3 -4 -5 -6arrow_forward
- 1. The table shows values of a function f(x). What is the average rate of change of f(x) over the interval from x = 5 to x = 9? Show your work. X 4 f(x) LO 5 6 7 8 9 10 -2 8 10 11 14 18arrow_forward• Find a real-world situation that can be represented by a sinusoidal function. You may find something online that represents a sinusoidal graph or you can create a sinusoidal graph yourself with a measuring tape and a rope. • Provide a graph complete with labels and units for the x- and y-axes. • Describe the amplitude, period, and vertical shift in terms of the real-world situation.arrow_forwardf(x) = 4x²+6x 2. Given g(x) = 2x² +13x+15 and find 41 (4)(x) Show your work.arrow_forward
- f(x) = x² − 6x + 8 3. Given and g(x) = x -2 solve f(x) = g(x) using a table of values. Show your work.arrow_forward1. Graph the function f(x) = 3√x-2 Answer: -6-5 -4-3-2 -1 6 LO 5 f(x) 4 3 2+ 1 1 2 3 4 5 6 -1 -2+ -3 -4 -5 -6- 56arrow_forwardA minivan is purchased for $29,248. The value of the vehicle depreciates over time. • Describe the advantages and disadvantages of using a linear function to represent the depreciation of the car over time. • Describe the advantages and disadvantages of using an exponential function to represent the depreciation of the car over time. • The minivan depreciates $3,000 in the first year. Write either a linear or exponential function to represent the value of the car x years after it was sold.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Lecture 46: Eigenvalues & Eigenvectors; Author: IIT Kharagpur July 2018;https://www.youtube.com/watch?v=h5urBuE4Xhg;License: Standard YouTube License, CC-BY
What is an Eigenvector?; Author: LeiosOS;https://www.youtube.com/watch?v=ue3yoeZvt8E;License: Standard YouTube License, CC-BY