Chapter 7, Problem 11P

Scores from a questionnaire measuring social anxiety form a normal distribution with a mean of μ = 50 and a standard deviation of σ = 10. What is the probability of obtaining a sample mean greater than M = 53.

1. a. for a random sample of n = 4 people?
2. b. for a random sample of n = 16 people?
3. c. for a random sample of n = 25 people?

To determine

The probability of obtaining a sample mean greater than $M=53$ for given sample.

Answer to Problem 11P

The probability of obtaining a sample mean greater than $M=53$ for given sample is 0.2743.

Explanation of Solution

Given info:

Numbers of people in a random sample are $n=4$.

Population mean is $\mu =50$.

Population standard deviation is $\sigma =10$.

Sample mean is $M=53$.

Calculation:

If $\mu$ and $\sigma$ represents the population mean and standard deviation respectively. Let n represents numbers of scores in each sample. Let M represents given sample mean. Then,

$\begin{array}{l}\mu =50\\ \sigma =10\\ n=4\\ M=53\end{array}$

Let $\overline{X}$ represents the random sample mean from given distribution. Let ${\mu }_M$ and ${\sigma }_M$ represents mean and standard error of $\overline{X}$ Then, expected mean of $\overline{X}$ will be same as population mean and standard error is calculated as:

$\begin{array}{c}{\mu }_M=50\\ {\sigma }_M=\frac{\sigma }{\sqrt{n}}\\ =\frac{10}{\sqrt{4}}\\ =5\end{array}$

Let p represents the probability that random mean is greater than $M=53$.

$\begin{array}{c}p=P(\overline{X}>53)\\ =1-P(\overline{X}<53)\end{array}$

Software procedure:

Step-by-step procedure to obtain the $\text{P(}\overline{\text{X}}\text{<53)}$ using the SPSS software:

• Click on first empty block of data view.
• Go to Transform>Choose Compute variable>Enter Probability in Target Variable.
• Choose CDF& Noncentral CDF under Function group> choose CDF.Normal> drag it to the numeric expression.
• Enter 53,50,5 in the braces of CDF.NORMAL
• Choose OK.

Output using the SPSS software is given below:

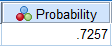
From the SPSS output, $\text{P(}\overline{\text{X}}\text{<53)}$ is 0.7257.

Using $\left(1\right)$ p is calculated as:

$\begin{array}{c}p=1-\text{P(}\overline{\text{X}}\text{<53)}\\ =1-0.7257\\ =0.2743\end{array}$

Thus, the probability of obtaining a mean greater than $M=53$ for given sample is 0.2743.

To determine

The probability of obtaining a sample mean greater than $M=53$ for given sample of $n=16$.

Answer to Problem 11P

The probability of obtaining a sample mean greater than $M=53$ for given sample is 0.1151.

Explanation of Solution

Given info:

Numbers of people in a random sample are $n=16$.

Population mean is $\mu =50$.

Population standard deviation is $\sigma =10$.

Sample mean is $M=53$.

Calculation:

If $\mu$ and $\sigma$ represents the population mean and standard deviation respectively. Let n represents numbers of scores in each sample. Let M represents given sample mean. Then,

$\begin{array}{l}\mu =50\\ \sigma =10\\ n=16\\ M=53\end{array}$

Let $\overline{X}$ represents the random sample mean from given distribution. Let ${\mu }_M$ and ${\sigma }_M$ represents mean and standard error of $\overline{X}$ Then, expected mean of $\overline{X}$ will be same as population mean and standard error is calculated as:

$\begin{array}{c}{\mu }_M=50\\ {\sigma }_M=\frac{\sigma }{\sqrt{n}}\\ =\frac{10}{\sqrt{16}}\\ =2.5\end{array}$

Let p represents the probability that random mean is greater than $M=53$.

$\begin{array}{c}p=P(\overline{X}>53)\\ =1-P(\overline{X}<53)\end{array}$

Software procedure:

Step-by-step procedure to obtain the $\text{P(}\overline{\text{X}}\text{<53)}$ using the SPSS software:

• Click on first empty block of data view.
• Go to Transform>Choose Compute variable>Enter Probability in Target Variable.
• Choose CDF& Noncentral CDF under Function group> choose CDF.Normal> drag it to the numeric expression.
• Enter 53,50,2.5 in the braces of CDF.NORMAL
• Choose OK.

Output using the SPSS software is given below:

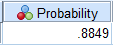
From the SPSS output, $\text{P(}\overline{\text{X}}\text{<53)}$ is 0.8849.

Thus,

$\begin{array}{c}p=1-\text{P(}\overline{\text{X}}\text{<53)}\\ =1-0.8849\\ =0.1151\end{array}$

Hence, the probability of obtaining a mean greater than $M=53$ for given sample is 0.1151.

To determine

The probability of obtaining a sample mean greater than $M=53$ for given sample $n=25$.

Answer to Problem 11P

The probability of obtaining a sample mean greater than $M=53$ for given sample is 0.0668.

Explanation of Solution

Given info:

Numbers of people in a random sample are $n=25$.

Population mean is $\mu =50$.

Population standard deviation is $\sigma =10$.

Sample mean is $M=53$.

Calculation:

If $\mu$ and $\sigma$ represents the population mean and standard deviation respectively. Let n represents numbers of scores in each sample. Let M represents given sample mean. Then,

$\begin{array}{l}\mu =50\\ \sigma =10\\ n=25\\ M=53\end{array}$

Let $\overline{X}$ represents the random sample mean from given distribution. Let ${\mu }_M$ and ${\sigma }_M$ represents mean and standard error of $\overline{X}$ Then, expected mean of $\overline{X}$ will be same as population mean and standard error is calculated as:

$\begin{array}{c}{\mu }_M=50\\ {\sigma }_M=\frac{\sigma }{\sqrt{n}}\\ =\frac{10}{\sqrt{25}}\\ =2\end{array}$

Let p represents the probability that random mean is greater than $M=53$.

$\begin{array}{c}p=P(\overline{X}>53)\\ =1-P(\overline{X}<53)\end{array}$

Software procedure:

Step-by-step procedure to obtain the $\text{P(}\overline{\text{X}}\text{<53)}$ using the SPSS software:

• Click on first empty block of data view.
• Go to Transform>Choose Compute variable>Enter Probability in Target Variable.
• Choose CDF& Noncentral CDF under Function group> choose CDF.Normal> drag it to the numeric expression.
• Enter 53,50,2 in the braces of CDF.NORMAL
• Choose OK.

Output using the SPSS software is given below:

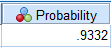
From the SPSS output, $\text{P(}\overline{\text{X}}\text{<53)}$ is 0.9332.

Thus,

$\begin{array}{c}p=1-\text{P(}\overline{\text{X}}\text{<53)}\\ =1-0.9332\\ =0.0668\end{array}$

Hence, the probability of obtaining a mean greater than $M=53$ for given sample is 0.0668.