Chapter 6.9, Problem 75ES

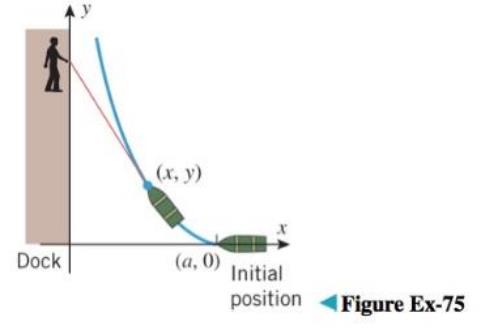
The accompanying figure shows a person pulling a boat by holding a rope of length a attached to the bow and walking along the edge of a dock. If we assume that the rope is always tangent to the curve traced by the bow of the boat, then this curve, which is called a tractrix, has the property that the segment of the tangent line between the curve and the $y\text{-axis}$ has a constant length $x$ . It can be proved that the equation of this tractrix is

$y=a{\mathrm{sech}}^{-1}\frac{x}{a}-\sqrt{a^2-x^2}$

(a) Show that to move the bow of the boat to a point $\left(x,y\right)$ , the person must walk a distance

$D=a{\mathrm{sech}}^{-1}\frac{x}{a}$

from the origin.

(b) If the rope has a length of $15\text{ m}$ , how far must the person walk from the origin to bring the boat $10\text{ m}$ from the dock? Round your answer to two decimal places.

(c) Find the distance traveled by the bow along the tractrix as it moves from its initial position to the point where it is $5\text{ m}$ from the dock.