Chapter 6.5, Problem 49E

(a)

To determine

To Find: The complex number that represent the position of the ship A and the ship B relative to the port.

Answer to Problem 49E

The position of the ship A in the form of the complex number is $3+4i$ .and B on the complex number is of the form $-5+2i$ .

Explanation of Solution

Given:

The imaginary positive imaginary axis as north and the positive real axis as east.

The ship A is 3 km east and 4 km north to the port.

The ship B is 5 km west and 2 km north.

The given Figure is shown in Figure 1

  

Figure 1

Calculation:

Consider the position of the ship in the complex plane is shown in Figure 2

  

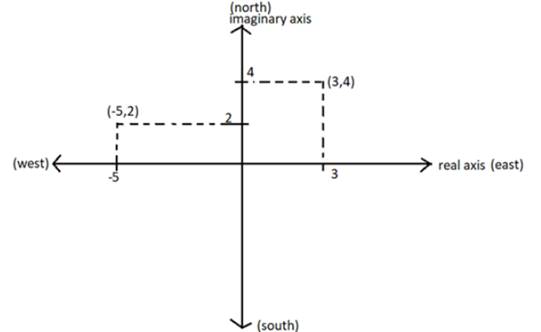
Figure 2

The position of the ship A is 3 km to the positive real axis and 4 km on the positive imaginary axis. Thus, the mean when the position is compare the point with the standard form of the complex number $a+bi$ the result obtained is $a=3$ and $b=4$ .

Thus, the position of the ship A in the form of the complex number is $3+4i$ .

In the same way the position of the ship B compared with the standard form $s+it$ . The value obtained is $s=-5$ and $t=2$ for the ship B .

Thus, the position of ship B on the complex number is of the form $-5+2i$ .

Thus, the position of the ship A in the form of the complex number is $3+4i$ .and B on the complex number is of the form $-5+2i$ .

(b)

To determine

To Find: The distance between the ship A and ship B.

Answer to Problem 49E

The distance between both the ships is $2\sqrt{17}$ km.

Explanation of Solution

Consider the position of the ship A is $3+4i$ and the ship B is $-5+2i$ .

Consider the distance formula is,

  $d=\sqrt{{\left(s-a\right)}^2+{\left(t-b\right)}^2}$

Then,

  $\begin{array}{c}d=\sqrt{{\left(-5-3\right)}^2+{\left(2-4\right)}^2}\\ =\sqrt{{\left(-8\right)}^2+{\left(-2\right)}^2}\\ =\sqrt{64+4}\\ =2\sqrt{17}\end{array}$

Thus, the distance between both the ships is $2\sqrt{17}$ km.