Mathematics for Machine Technology
7th Edition
ISBN: 9781133281450
Author: John C. Peterson, Robert D. Smith
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 65, Problem 12A
Refer to Figure 65-3 in answering exercises 1 through 7. It may be helpful to sketch figures.
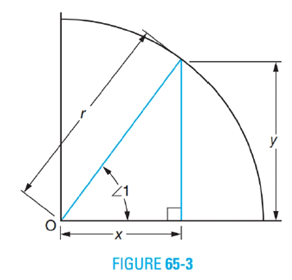
12. When
a. What is the value of the sine function?
b. What is the value of the secant function?
c. What is the value of the cosine function?
d. What is the value of the tangent function?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Evaluate the following integrals, where in each case y is the unit circle taken once
anticlockwise. (Standard results may be quoted without proof.)
(i) [|z|dz
(ii) L
cos(1/2)
dz;
(iii) z +31² dz;
(iv)
L
exp(22)
tan z dz;
dz.
z(x+4)
State Liouville's Theorem on entire functions and the Maximum Modulus Principle.
Let p(z) = z″ + an−12″ ¹ + ... + a1z + ao be a nonconstant polynomial. Show
that there is a number R> 0 such that
|2|n
|p(z)|≥
for |z|> R.
2
By considering f(z) =
in C.
P(2)
and using the results above, deduce that p has a zero
A power series Σan has radius of convergence R > 0 and defines a function
f(z) on {z C || < R}. Write down the power series for the functions f'(z)
and f(22), and state without proof their radii of convergence.
Show that there is an entire function ƒ : C→ C, expressible as the sum of a power
series, such that
f(0) = 0, f'(0) = 0, and f"(z) = exp(22) for all z Є C.
Chapter 65 Solutions
Mathematics for Machine Technology
Ch. 65 - If tan A=4.13792 , determine the value of angle A...Ch. 65 - Find the number of cubic inches of material...Ch. 65 - Find the number of cubic inches of material...Ch. 65 - The sector of a circle has an area of 231.3 sq in....Ch. 65 - Determine the arc length ABC if r=5.75in. and...Ch. 65 - Identify each of the following angles as acute....Ch. 65 - Prob. 7ACh. 65 - Refer to Figure 65-3 in answering exercises 1...Ch. 65 - Prob. 9ACh. 65 - Refer to Figure 65-3 in answering exercises 1...
Ch. 65 - Prob. 11ACh. 65 - Refer to Figure 65-3 in answering exercises 1...Ch. 65 - Prob. 13ACh. 65 - For each exercise, functions of two angles are...Ch. 65 - For each exercise, functions of two angles are...Ch. 65 - For each exercise, functions of two angles are...Ch. 65 - For each exercise, functions of two angles are...Ch. 65 - For each exercise, functions of two angles are...Ch. 65 - For each exercise, functions of two angles are...Ch. 65 - For each exercise, functions of two angles are...Ch. 65 - For each exercise, functions of two angles are...Ch. 65 - For each exercise, functions of two angles are...Ch. 65 - For each exercise, functions of two angles are...Ch. 65 - For each exercise, functions of two angles are...Ch. 65 - Prob. 25ACh. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - Prob. 41ACh. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - For each function of an angle, write the...Ch. 65 - Prob. 45ACh. 65 - For each exercise, functions and cofunctions of...Ch. 65 - Prob. 47ACh. 65 - For each exercise, functions and cofunctions of...Ch. 65 - Prob. 49ACh. 65 - For each exercise, functions and cofunctions of...Ch. 65 - Prob. 51ACh. 65 - For each exercise, functions and cofunctions of...Ch. 65 - Prob. 53ACh. 65 - For each exercise, functions and cofunctions of...Ch. 65 - Prob. 55ACh. 65 - For each exercise, functions and cofunctions of...Ch. 65 - Prob. 57A
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- A polynomial p of degree n has all its zeros in the disc of radius R centred at 0. Quoting a theorem from the course, write down the value of 1 2πί La P(z) 'p'(z) dz, where is the circle of radius 2R centred at 0. γarrow_forwardCalculate the following integrals using complex variable techniques. ᏧᎾ 2π (i) S 1+8 cos20 (ii) I COS x dz x²-2x+5 Leave your answers in terms of real functions of real variables.arrow_forwardFor each of the following functions determine whether it is the real part of a differentiable function defined on C. If it is, determine a corresponding imaginary part. (i) u(x, y) = x² - y²+4xy; (ii) u(x, y) = x³ — y³ + 3x²y. -arrow_forward
- Let A be an algebra and X C A a subset. Recall that the centraliser of X in A is defined to be == C(X) = {a A | ax = xa for all x = X}. Let U = { (o b) : a, b, c & R} ≤ M₂(R). C as in Question 1. (i) Show that the centraliser of U in M₂(R) is: C(U) = {(o 9 ) ; a € R} . 0 : (ii) Let M=R2, the natural module for U. Show that Endu (M) = R. (iii) Find all one-dimensional submodules of M. (iv) Is MXY for some submodules X, Y of M? (no proof is required for this part.)arrow_forwardLet A be a finite-dimensional algebra. Prove that A is a semisimple algebra if and only if every left ideal I of A admits a complement (so there exists a left ideal J such that A = I J as vector spaces). You I may assume that if a module M can be written as a sum of simple modules M = S₁+ S₂++ Sn, then we can find a subset R C {1, 2, ………, n} such that DER ST is a direct sum of simples. You may also assume that every non-zero finite-dimensional module has a simple submodule. M =arrow_forwardShow that these two matrices generate the algebra M₂(Q) over the field Q. 0 1 S := and T = == -1 - -1 (13)arrow_forward
- Let G = S3, the symmetric group on 3 letters. Show that K(X,Y) KG - (X21, YX XY², Y³ —– 1) ' - (Hint: Write S3 (12) and Y X S3 as a group.) = {id, (12), (23), (13), (123), (132)}. Consider the map from → (123). You may assume that these two elements generatearrow_forwardConsider a simplified two-joint robotic arm where the two joints are connected by rigid links.Each joint has a mass, and the links are modeled as idealized rods. The motion of each jointaffects the other through the coupling of forces. The system can be modeled by the followingsecond-order coupled ODEs: m1θ1" + k1(θ1 − θrest) + k3(θ1 − θ2) = 0 (equation 1)m2θ2" + k2(θ2 − θrest) + k3(θ2 − θ1) = 0 (equation 2) where θ1(t) and θ2(t) represent the angular positions of the first and second joints, respec-tively. m1 and m2 are the effective masses at each joint. k1, k2 and k3 are the stiffnessconstants representing the elastic restoring forces in the joints and links. θrest = 0 representsthe equilibrium position for each joint.The parameters are:m1 = 1, m2 = 1, θrest = 0, k1 = 1, k2 = 2, k3 = 3, θrest = 0The initial conditions are:θ1(0) = 1, θ2(0) = 2Please solve by hand to get θ1(t) and θ2(t) using eigenvectors and eigenvalues. Show all steps/calculations, and provide a written description…arrow_forward3feet in 1secound; 21feet in x secondsarrow_forward
- (15 pts) Show your work to get full credit! Compute a QR factorization of the matrixarrow_forward(5) Let G be a group. Show that G acts on itself via the action g⚫a (i.e. using the binary operation of G) for all g, a Є G. [ for each of the three axioms, plus 1 for conclusion] = gaarrow_forward= (2) Let H {id, (12) (34), (13)(24), (14)(23)}. Prove that H is a sub- group of the symmetric group S4 of degree 4. each of the four axioms, plus 1 for the conclusion] 1 forarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Fundamental Trigonometric Identities: Reciprocal, Quotient, and Pythagorean Identities; Author: Mathispower4u;https://www.youtube.com/watch?v=OmJ5fxyXrfg;License: Standard YouTube License, CC-BY