
Concept explainers
Blood pressure: High blood pressure has been identified as a risk factor for heart attacks and strokes. The National Health and Nutrition Examination Survey reported that the proportion of U.S. adults with high blood pressure is 0.3. A sample of 38 U.S. adults is chosen.
- a. Is it appropriate to use the normal approximation to find the
probability that more than 40% of the people in the sample have high blood pressure? If so, find the probability. If not, explain why not. - b. A new sample of 80 adults is drawn. Find the probability that more than 40% of the people in this sample have high blood pressure.
- c. Find the probability that the proportion of individuals in the sample of 80 who have high blood pressure is between 0.20 and 0.35.
- d. Find the probability that less than 25% of the people in the sample of 80 have high blood pressure.
- e. Would it be unusual if more than 45% of the individuals in the sample of 80 had high blood pressure?
a.
Check whether it is appropriate to use the normal approximation to find the probability that more than 40% of the people in the sample have high blood pressure and if it is appropriate find the probability, if not explain the reason.
Answer to Problem 22E
Yes, it is appropriate to use the normal approximation.
The probability that more than 40% of the people in the sample have high blood pressure is 0.0893.
Explanation of Solution
Calculation:
The given information is that the sample of U.S. adults chosen (n) is 38 and the proportion of U.S. adults with high blood pressure (p) is 0.3.
Central Limit Theorem of proportions:
If
Requirement check:
Condition 1:
Condition 2:
Condition 1:
Substitute 38 for n and 0.3 for p in np,
Thus, the requirement
Condition 2:
Substitute 38 for n and 0.3 for p in
Thus, the requirement of
Here, both the requirements are satisfied. Thus, it is appropriate to use the normal approximation.
Hence, the normal approximation is appropriate to use for finding the probability that more than 40% of the people in the sample have high blood pressure.
For mean
Substitute
Thus, the value of
For standard deviation
Substitute
Thus, the value of
The probability that more than 40% of the people in the sample have high blood pressure represents the area to the right of 0.40
Software Procedure:
Step by step procedure to find the probability by using MINITAB software is as follows:
- Choose Graph > Probability Distribution Plot > View Probability > OK.
- From Distribution, choose ‘Normal’ distribution.
- Enter Mean as 0.3 and Standard deviation as 0.07434.
- Click the Shaded Area tab.
- Choose X value and Right Tail for the region of the curve to shade.
- Enter the X value as 0.40.
- Click OK.
Output using MINITAB software is as follows:
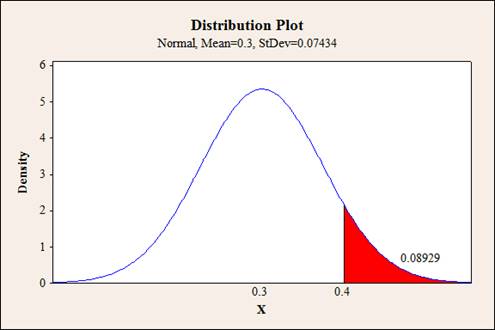
From the output, it can be observed that the probability that more than 40% of the people in the sample have high blood pressure is approximately 0.0893.
b.
Find the probability that more than 40% of the people in the sample have high blood pressure.
Answer to Problem 22E
The probability that more than 40% of the people in the sample have high blood pressure is 0.0255.
Explanation of Solution
Calculation:
The given information is that the sample of U.S. adults is chosen (n) is 80 and the proportion of U.S. adults with high blood pressure (p) is 0.3.
If
Substitute
Thus, the mean
The formula for finding standard deviation
Substitute
Thus, the value of
The probability that more than 40% of the people in the sample have high blood pressure represents the area to the right of 0.40
Software Procedure:
Step by step procedure to find the probability by using MINITAB software is as follows:
- Choose Graph > Probability Distribution Plot > View Probability > OK.
- From Distribution, choose ‘Normal’ distribution.
- Enter Mean as 0.3 and Standard deviation as 0.05123.
- Click the Shaded Area tab.
- Choose X value and Right Tail for the region of the curve to shade.
- Enter the X value as 0.40.
- Click OK.
Output using MINITAB software is as follows:

From the output, it can be observed that the probability that more than 40% of the people in the sample have high blood pressure is approximately 0.0255.
c.
Find the probability that the proportion of individuals in the sample of 80 who have high blood pressure is between 0.20 and 0.35.
Answer to Problem 22E
The probability that the proportion of individuals in the sample of 80 who have high blood pressure is between 0.20 and 0.35 is 0.8100.
Explanation of Solution
Calculation:
The probability that the proportion of individuals in the sample of 80 who have high blood pressure is between 0.20 and 0.35 represents the area to the right of 0.20 and the area to the left of 0.35.
Software Procedure:
Step by step procedure to find the probability by using MINITAB software is as follows:
- Choose Graph > Probability Distribution Plot > View Probability > OK.
- From Distribution, choose ‘Normal’ distribution.
- Enter Mean as 0.3 and Standard deviation as 0.05123.
- Click the Shaded Area tab.
- Choose X value and Middle for the region of the curve to shade.
- Enter the X value 1 as 0.20 and X value 2 as 0.35.
- Click OK.
Output using MINITAB software is as follows:
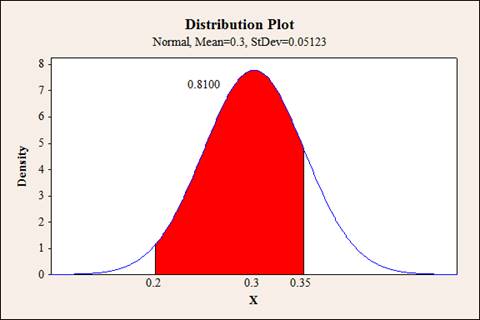
From the output, it can be observed that the probability that the proportion of individuals in the sample of 80 who have high blood pressure is between 0.20 and 0.35 is 0.8100.
d.
Find the probability that less than 25% of the people in the sample of 80 have high blood pressure.
Answer to Problem 22E
The probability that less than 25% of the people in the sample of 80 have high blood pressure is 0.1645.
Explanation of Solution
Calculation:
The probability that less than 25% of the people in the sample of 80 have high blood pressure represents the area to the left of 0.25
Software Procedure:
Step by step procedure to find the probability by using MINITAB software is as follows:
- Choose Graph > Probability Distribution Plot > View Probability > OK.
- From Distribution, choose ‘Normal’ distribution.
- Enter Mean as 0.3 and Standard deviation as 0.05123.
- Click the Shaded Area tab.
- Choose X value and Left Tail for the region of the curve to shade.
- Enter the X value as 0.25.
- Click OK.
Output using MINITAB software is as follows:

From the output, it can be observed that the probability that less than 25% of the people in the sample of 80 have high blood pressure is 0.1645.
e.
Check whether it is unusual if more than 45% of the individuals in the sample of 80 had high blood pressure.
Answer to Problem 22E
Yes, it is unusual if more than 45% of the individuals in the sample of 80 had high blood pressure.
Explanation of Solution
Calculation:
Unusual:
If the probability of an event is less than 0.05 then the event is called unusual.
The probability of more than 45% of the individuals in the sample of 80 had high blood pressure represents the area to the right of 0.45.
Software Procedure:
Step by step procedure to find the probability by using MINITAB software is as follows:
- Choose Graph > Probability Distribution Plot > View Probability > OK.
- From Distribution, choose ‘Normal’ distribution.
- Enter Mean as 0.3 and Standard deviation as 0.05123.
- Click the Shaded Area tab.
- Choose X value and Right Tail for the region of the curve to shade.
- Enter the X value as 0.45.
- Click OK.
Output using MINITAB software is as follows:
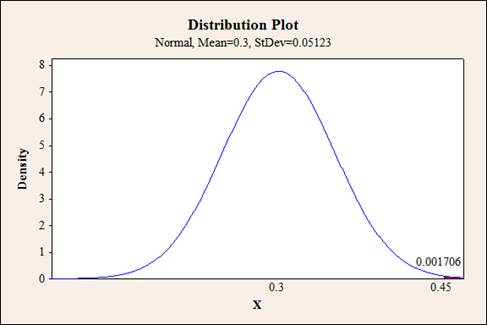
From the output, it can be observed that the probability of more than 45% of the individuals in the sample of 80 had high blood pressure is approximately 0.0017.
Here, the probability of more than 45% of the individuals in the sample of 80 had high blood pressure is less than 0.05. That is,
Want to see more full solutions like this?
Chapter 6 Solutions
Essential Statistics
- Cycles to failure Position in ascending order 0.5 f(x)) (x;) Problem 44 Marsha, a renowned cake scientist, is trying to determine how long different cakes can survive intense fork attacks before collapsing into crumbs. To simulate real-world cake consumption, she designs a test where cakes are subjected to repeated fork stabs and bites, mimicking the brutal reality of birthday parties. After rigorous testing, Marsha records 10 observations of how many stabs each cake endured before structural failure. Construct P-P plots for (a.) a normal distribution, (b.) a lognormal distribution, and (c.) a Weibull distribution (using the information included in the table below). Which distribution seems to be the best model for the cycles to failure for this material? Explain your answer in detail. Observation Empirical cumulative Probability distribution Cumulative distribution Inverse of cumulative distribution F-1 (-0.5) F(x)) (S) n 4 3 1 0.05 9 5 2 0.15 7 7 3 0.25 1 10 4 0.35 3 12 5 0.45 Normal…arrow_forwardProblem 3 In their lab, engineer Daniel and Paulina are desperately trying to perfect time travel. But the problem is that their machine still struggles with power inconsistencies-sometimes generating too little energy, other times too much, causing unstable time jumps. To prevent catastrophic misjumps into the Jurassic era or the far future, they must calibrate the machine's power output. After extensive testing, they found that the time machine's power output follows a normal distribution, with an average energy level of 8.7 gigawatts and a standard deviation of 1.2 gigawatts. The Time Travel Safety Board has set strict guidelines: For a successful time jump, the machine's power must be between 8.5 and 9.5 gigawatts. What is the probability that a randomly selected time jump meets this precision requirement? Daniel suggests that adjusting the mean power output could improve time-travel accuracy. Can adjusting the mean reduce the number of dangerous misjumps? If yes, what should the…arrow_forwardProblem 5 ( Marybeth is also interested in the experiment from Problem 2 (associated with the enhancements for Captain America's shield), so she decides to start a detailed literature review on the subject. Among others, she found a paper where they used a 2"(4-1) fractional factorial design in the factors: (A) shield material, (B) throwing mechanism, (C) edge modification, and (D) handle adjustment. The experimental design used in the paper is shown in the table below. a. Run A B с D 1 (1) -1 -1 -1 1 2 a 1 -1 -1 1 3 bd -1 1 -1 1 4 abd 1 1 -1 1 5 cd -1 -1 1 -1 6 acd 1 -1 1 -1 7 bc -1 1 1 -1 abc 1 1 1 -1 paper? s) What was the generator used in the 2"(4-1) fractional factorial design described in the b. Based on the resolution of this design, what do you think about the generator used in the paper? Do you think it was a good choice, or would you have selected a different one? Explain your answer in detail.arrow_forward
- Suppose we wish to test the hypothesis that women with a sister’s history of breast cancer are at higher risk of developing breast cancer themselves. Suppose we assume that the prevalence rate of breast cancer is 3% among 60- to 64-year-old U.S. women, whereas it is 5% among women with a sister history. We propose to interview 400 women 40 to 64 years of age with a sister history of the disease. What is the power of such a study assuming that the level of significance is 10%? I only need help writing the null and alternative hypotheses.arrow_forward4.96 The breaking strengths for 1-foot-square samples of a particular synthetic fabric are approximately normally distributed with a mean of 2,250 pounds per square inch (psi) and a standard deviation of 10.2 psi. Find the probability of selecting a 1-foot-square sample of material at random that on testing would have a breaking strength in excess of 2,265 psi.4.97 Refer to Exercise 4.96. Suppose that a new synthetic fabric has been developed that may have a different mean breaking strength. A random sample of 15 1-foot sections is obtained, and each section is tested for breaking strength. If we assume that the population standard deviation for the new fabric is identical to that for the old fabric, describe the sampling distribution forybased on random samples of 15 1-foot sections of new fabricarrow_forwardUne Entreprise œuvrant dans le domaine du multividéo donne l'opportunité à ses programmeurs-analystes d'évaluer la performance des cadres supérieurs. Voici les résultats obtenues (sur une échelle de 10 à 50) où 50 représentent une excellente performance. 10 programmeurs furent sélectionnés au hazard pour évaluer deux cadres. Un rapport Excel est également fourni. Programmeurs Cadre A Cadre B 1 34 36 2 32 34 3 18 19 33 38 19 21 21 23 7 35 34 8 20 20 9 34 34 10 36 34 Test d'égalité des espérances: observations pairéesarrow_forward
- A television news channel samples 25 gas stations from its local area and uses the results to estimate the average gas price for the state. What’s wrong with its margin of error?arrow_forwardYou’re fed up with keeping Fido locked inside, so you conduct a mail survey to find out people’s opinions on the new dog barking ordinance in a certain city. Of the 10,000 people who receive surveys, 1,000 respond, and only 80 are in favor of it. You calculate the margin of error to be 1.2 percent. Explain why this reported margin of error is misleading.arrow_forwardYou find out that the dietary scale you use each day is off by a factor of 2 ounces (over — at least that’s what you say!). The margin of error for your scale was plus or minus 0.5 ounces before you found this out. What’s the margin of error now?arrow_forward
- Suppose that Sue and Bill each make a confidence interval out of the same data set, but Sue wants a confidence level of 80 percent compared to Bill’s 90 percent. How do their margins of error compare?arrow_forwardSuppose that you conduct a study twice, and the second time you use four times as many people as you did the first time. How does the change affect your margin of error? (Assume the other components remain constant.)arrow_forwardOut of a sample of 200 babysitters, 70 percent are girls, and 30 percent are guys. What’s the margin of error for the percentage of female babysitters? Assume 95 percent confidence.What’s the margin of error for the percentage of male babysitters? Assume 95 percent confidence.arrow_forward

 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill


