
Find the area of this figure. Round your answer to 2 decimal places.
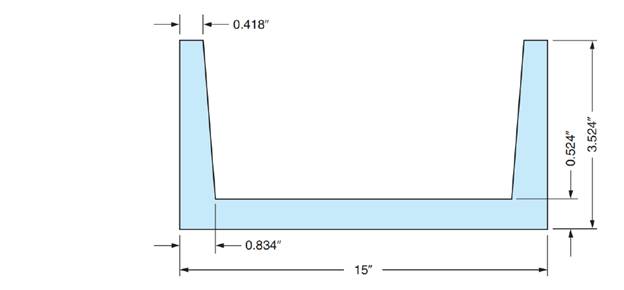
Area of given figure round to 2 decimal places.
Answer to Problem 1A
Area of given figure is
Explanation of Solution
Given:
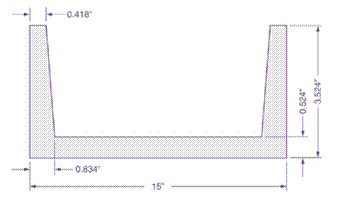
The shaded diagram is represented as:
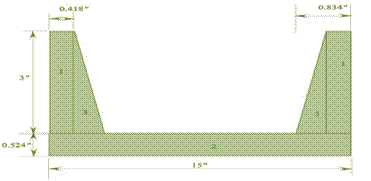
The above diagram is divided into three parts.
The area of diagram can be calculated as:
Now
Then
Then
Substitute the values of
Therefore, the area of given figure is
Want to see more full solutions like this?
Chapter 60 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
Math in Our World
Pathways To Math Literacy (looseleaf)
College Algebra Essentials (5th Edition)
College Algebra (Collegiate Math)
- 6. Use Laplace transform to find the solution of the initial value problem. (a) y" +4y' + 4y = 0; (b) y(4)-4y=0; y(0) = 0, y(0) = 1, y'(0) = 1 y'(0) = 1, y"(0) = 0, y" (0) = 2 1arrow_forwardFind An of the cosine series. Could you see if my working is correct? I've attached it with the questionarrow_forwardQ5 Using Hermite's algorithm find s, t = Z so that s² + t² = 101.arrow_forward
- Q4. Find all solutions of 91x² + y² = 1 with x, y Є Z.arrow_forwardQ3. Find all solutions of x² - 29y² = ±1 with x, y ɛ Z.arrow_forwardProblem 11 (Gram-Schmidt). Try the Gram-Schmidt procedure for the vectors, 1 0 2 with respect to the standard dot product on R4. What happens? Can you explain why you are unable to complete the algorithm? Problem 12 (Orthogonal Matrices Preserve Orthogonality). Suppose x, y = Rn" are orthogonal to each other with respect to some inner product (.,.) and that A is an orthogonal matrix and B is some invertible matrix. 1. Prove that Ax and Ay are also orthogonal to each other and that ||x|| = ||Ax|| and ||y|| : = ||Ay||. 2. Is it true that Bx and By are also orthogonal to each other and that ||x|| = ||Bx|| and ||y|| = = ||By||? Provide a proof or a counter-example. Problem 13 (Orthogonal Complement). Let W be the subspace of R5 spanned by, 1 2 2 4 u = 3 , v= 7 2 2 Find a basis of the orthogonal complement W- of W. Verify in this particular example that WW₁ = {0} and that dim(W) + dim(W¹) = 5.arrow_forward
- Problem 5 (Rank-Nullity Theorem). Let T : P3 → M2×2 be defined as, T(p(x)) P(0) p'(1)] = 1. Prove that T is a linear transformation. 2. Find ker(T). Is T injective? 3. Find im(T). Is T surjective? 4. Verify the Rank-Nullity Theorem for T. Problem 6 (Change of Basis). Let B₁ = polynomials in P3. - - {1, x, x², x³} and B₁ = {1, x, x(x − 1), x(x − 1)(x − 2)} be two sets of 1. Is B2 a basis for P3? Justify your answer. 2. Find SB₁→B₂ and SB2→B₁. Which one is "easier" to find? - Problem 7 (Change of Basis). Let B₁ = {eª, sin² (x), cos² (x)} and B₁ = {e*, sin(2x)}. Recall that sin(20) = 2 sin(0) cos(0). Suppose V = span (B₁) and W = span(B2). Let T: VW be a linear transformation defined as T(f(x)) = f'(x). 1 1. Prove that B₁ is a basis. 2. Let g(x) = 5 - 3e. Show that g = V and find T(g(x)). 3. Find [TB₁B2 4. Is T injective? 5. Is T surjective?arrow_forwardProblem 14 (Orthogonal Matrices). Prove each of the following. 1. P is orthogonal PT is orthogonal. 2. If P is orthogonal, then P-1 is orthogonal. 3. If P, Q are orthogonal, then PQ is orthogonal. Problem 15 (Orthogonal Complement). Consider P2 with the inner product, (f,g) = f(x)g(x)dx. Put W = span(2x+1). Find a basis of W. (1)arrow_forwardProblem 8 (Diagonalization). Let T : P₂ → P₂ be defined as, T(p(x)) = xp'(x). 1. Find the eigenvalues and eigenvectors of T. 2. Show that T is diagonalizable and write P2 as the sum of the eigenspaces of T. Problem 9 (Basis). Determine all the values of the scalar k for which the following four matrices form a basis for M2×2: A₁ = , A2 = k -3 0 , A3 = [ 1 0 -k 2 0 k " A₁ = . -1 -2 Problem 10 (Orthogonality). In this question, we will again see how orthogonality makes computations sim- pler. 1. Let u1,..., un be an (ONB) of a finite-dimensional inner product space V. Let v = c₁u₁ + ... + Сnun and w = d¹µ₁ + ... + dnUn be any two elements of V. Prove that (v, w) = c₁d₁ + ... + Cndn. 2. Write down the corresponding inner product formula for an orthogonal basis.arrow_forward
- Let 01(x) = * 0(t) dt, for x > 1, where 0 is Chebyshev's function. Let A1(n) = log n if n is prime, and A₁(n) = 0 otherwise. Prove that 01(x) = (x − n) A1(n), narrow_forwardLet 01 (x) = [* 0(t) dt, for x > 1, where 0 is Chebyshev's function. Let = lim 01(x)/x². 1+00 By considering (t) dt, prove that T-ET 01(x) 01(x Ex) Ex-(x), where = (> 0) is small. - Assuming that 0(x)/x →1 as x → ∞, deduce that (1-1) ≤ 1. By similarly considering (t) dt, prove that (1+½)1 ≥1. 2 Deduce that 01(x) 1½². 2arrow_forwardConsider a rectangular membrane with fixed boundaries of dimensions 5 (horizontal) by 3 (vertical). The deflection u(x, y, t) satisfies the equation utt = 6(uxx + Uyy). (a) Find a formula for the deflection u(x, y, t), if the initial velocity g(x, y) is zero and the initial displacement f(x, y) is f(x, y) = u(x, y, 0) = 2 sin(5πx) sin(лy) - 4 sin(2x) sin(3лy) Do not show the separation of variables. Start with the formula for u(x, y, t). You need to show all details of integration or superposition (if it applies) for credit. (b) Find a numerical approximation for u(5/2, 3/2, 2).arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,





