
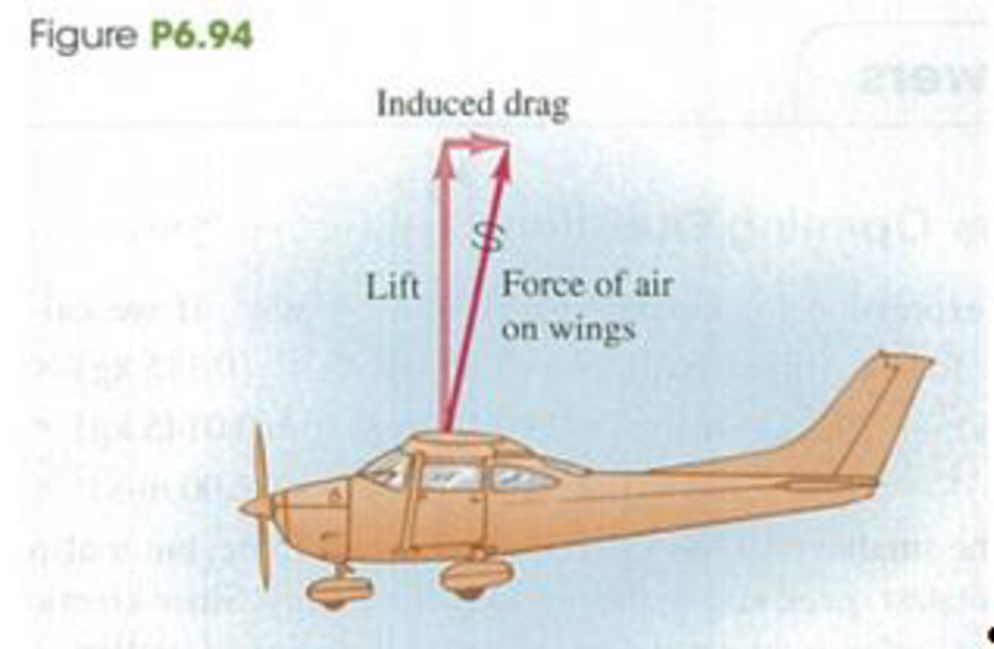
CALC An airplane in flight is subject to an air resistance force proportional to the square of its speed v. But there is an additional resistive force because the airplane has wings. Air flowing over the wings is pushed down and slightly forward, so from Newton’s third law the air exerts a force on the wings and airplane that is up and slightly backward (Fig. P6.94). The upward force is the lift force that keeps the airplane aloft, and the backward force is called induced drag. At flying speeds, induced drag is inversely proportional to υ2, so the total air resistance force can be expressed by Fsir = α υ2 + β/υ2. where α and β are positive constants that depend on the shape and size of the airplane and the density of the air. For a Cessna 150, a small single-engine airplane, α = 0.30 N • s2/m2 and β = 3.5 × 105 N • m2/s2. In steady flight, the engine must provide a forward force that exactly balances the air resistance force, (a) Calculate the speed (in km/h) at which this airplane will have the maximum range (that is. travel the greatest distance) for a given quantity of fuel, (b) Calculate the speed (in km/h) for which the airplane will have the maximum endurance (that is, remain in the air the longest time).
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
University Physics (14th Edition)
Additional Science Textbook Solutions
Biology: Life on Earth with Physiology (11th Edition)
Anatomy & Physiology (6th Edition)
Human Biology: Concepts and Current Issues (8th Edition)
Cosmic Perspective Fundamentals
Campbell Essential Biology with Physiology (5th Edition)
Chemistry: Structure and Properties (2nd Edition)
- I need help with part B. I cant seem to get the correct answer. Please walk me through what youre doing to get to the answer and what that could bearrow_forwardQuestion 6: Chlorine is widely used to purify municipal water supplies and to treat swimming pool waters. Suppose that the volume of a particular sample of Cl₂ gas is 8.70 L at 895 torr and 24°C. (a) How many grams of Cl₂ are in the sample? ⚫ Atomic mass of CI = 35.453 g/mol • Molar mass of Cl₂ = 2 x 35.453 = 70.906 g/mol Solution: Use the Ideal Gas Law: Step 1: Convert Given Values • Pressure: P = 895 torr → atm PV= = nRT 1 P = 895 × = 1.1789 atm 760 • Temperature: Convert to Kelvin: T24273.15 = 297.15 K • Gas constant: R = 0.0821 L atm/mol. K Volume: V = 8.70 L Step 2: Solve for n . PV n = RT n = (1.1789)(8.70) (0.0821)(297.15) 10.25 n = = 0.420 mol 24.405 Step 3: Calculate Mass of Cl₂ Final Answer: 29.78 g of Cl₂. mass nx M mass= (0.420)(70.906) mass= 29.78 garrow_forwardE1 R₁ w 0.50 20 Ω 12 R₁₂ ww ΒΩ R₂ 60 E3 C RA w 15 Ω E2 0.25 E4 0.75 Ω 0.5 Ωarrow_forward
- What is the force (in N) on the 2.0 μC charge placed at the center of the square shown below? (Express your answer in vector form.) 5.0 με 4.0 με 2.0 με + 1.0 m 1.0 m -40 με 2.0 μCarrow_forwardWhat is the force (in N) on the 5.4 µC charge shown below? (Express your answer in vector form.) −3.1 µC5.4 µC9.2 µC6.4 µCarrow_forwardAn ideal gas in a sealed container starts out at a pressure of 8900 N/m2 and a volume of 5.7 m3. If the gas expands to a volume of 6.3 m3 while the pressure is held constant (still at 8900 N/m2), how much work is done by the gas? Give your answer as the number of Joules.arrow_forward
 College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





